Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Berger, Ruth I
1991.
Quadratic extensions with elementary abelian K2(O).
Journal of Algebra,
Vol. 142,
Issue. 2,
p.
394.
Conner, P.E.
and
Hurrelbrink, Jurgen
2001.
On the 4-rank of the Tame Kernel K2(O) in Positive Definite Terms.
Journal of Number Theory,
Vol. 88,
Issue. 2,
p.
263.
Yue, Qin
2002.
Dyadic ideal, class group, and tame kernel in quadratic fields.
Journal of Pure and Applied Algebra,
Vol. 166,
Issue. 1-2,
p.
229.
Dubois, I.
and
Soriano-Gafiuk, F.
2004.
Un nouveau régulateur de type Gross.
Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg,
Vol. 74,
Issue. 1,
p.
89.
Qin, Hourong
2005.
The 2-Sylow subgroup of K2OF for number fields F.
Journal of Algebra,
Vol. 284,
Issue. 2,
p.
494.
Yin, Xiaobin
Qin, Hourong
and
Zhu, Qunsheng
2008.
The Structure of the Tame Kernels of Quadratic Number Fields (III).
Communications in Algebra,
Vol. 36,
Issue. 3,
p.
1012.


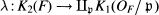 with a finite kernel, which is called the tame kernel, isomorphic to
with a finite kernel, which is called the tame kernel, isomorphic to 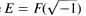 and
and 