Impact statement
Sandy beach morphology exhibits a large variability in space and time. Closely associated with such morphological variability are changes in the surf zone processes, such as type of wave breaking, wave energy gradients, strength and character of nearshore currents and modes of sediment transport. The beach model morphodynamic framework of Wright and Short (1984) captures this mutual feedback between morphological and hydrodynamic variabilities, and describes the occurrence of beach types across the complete reflective–dissipative spectrum. In this review, we provide this framework with a stronger physical underpinning by drawing on the results of several decades of coastal research, whilst also highlighting existing gaps in our knowledge and providing future perspectives. This review will provide physical coastal researchers with an enhanced morphodynamic framework within which to place their beach research and interpret their results, as well as providing them with suggestions for future research. However, sandy beaches are not only of interest and of relevance to physical coastal researchers, because beach morphodynamics directly affects, amongst others, beach ecology, pollutant dispersal in the surf zone and beach hazards. Anyone involved with these processes, either from a scientific or management point of view, will benefit from the enhanced beach model morphodynamic framework presented in this review.
Introduction
Wave-dominated sandy beaches occur on all continents (Luijendijk et al. Reference Luijendijk, Hagenaars, Ranasinghe, Baart, Donchyts and Aarninkhof2018) and are amongst the world’s most energetic and dynamic environments. They are highly valued by society as they attract many visitors and contribute significantly to local, regional or even national economies (Houston Reference Houston2018; Garola et al. Reference Garola, López-Dóriga and Jiménez2022). They also represent natural forms of coastal protection against flooding; therefore, beach nourishment is increasingly seen as a sustainable means of coastal adaptation to climate change (de Schipper et al. Reference de Schipper, Ludka, Raubenheimer, Luijendijk and Schlacher2020). Although historically referred to as ecological deserts, it is now recognised that sandy beaches support a diverse beach fauna (McLachlan et al. Reference McLachlan, Defeo and Short2018) and that surf zones are nursing grounds for many fish species (Ciotti et al. Reference Ciotti, Targett, Nash and Burrows2013). Beaches can also be dangerous environments for beach users (West Reference West and Schwartz2005), especially when rip currents are present (Brighton et al. Reference Brighton, Sherker, Brander, Thompson and Bradstreet2013), and there is a direct link between the type of beach and the beach hazard level (Scott et al. Reference Scott, Masselink and Russell2011). Finally, beaches interact strongly with sandy dune systems, as dune development and beach–dune sediment exchange are closely related to beach state and surf zone processes (Walker et al. Reference Walker, Davidson-Arnott, Bauer, Hesp, Delgado-Fernandez, Ollerhead and Smyth2017; Cohn et al. Reference Cohn, Hoonhout, Goldstein, De Vries, Moore, Durán Vinent and Ruggiero2019).
Beach morphodynamics refers to the mutual interactions between beach morphology and hydrodynamic processes (including wave, tide and wave-driven currents) involving the motion of sediment (Figure 1a). On any given beach, temporal changes in morphology can be forced by variability in the hydrodynamic conditions operating on a range of timescales (see Figure 1b; Cowell et al. Reference Cowell, Thom, van de Plassche, RWG and Woodroffe1995), including over individual waves (Blenkinsopp et al. Reference Blenkinsopp, Turner, Masselink and Russell2011), tidal cycles (Almeida et al. Reference Almeida, Masselink, Russell and Davidson2015), storms (Harley et al. Reference Harley, Turner, Kinsela, Middleton, Mumford, Splinter, Phillips, Simmons, Hanslow and Short2017) and seasons (Masselink and Pattiaratchi Reference Masselink and Pattiaratchi2001). Over even longer periods, the integrated result of alternating storm sequences and recovery periods can give rise to multiannual changes in beach morphology (Dodet et al. Reference Dodet, Castelle, Masselink, Scott, Davidson, Floc’h, Jackson and Suanez2018; Vos et al. Reference Vos, Harley, Splinter, Simmons and Turner2019) linked with climate modes of atmospheric variability. Along any stretch of coastline, spatial changes in beach morphology are related to along-coast variability in the hydrodynamic conditions, mostly wave exposure, but also geographic variation in sediment characteristics, geological framework and tidal regime (Jackson et al. Reference Jackson, Cooper and Río2005; Scott et al. Reference Scott, Masselink and Russell2011; Aleman et al. Reference Aleman, Robin, Certain, Anthony and Barusseau2015). Spatial and temporal variability in beach morphology has long been considered within the morphodynamic framework of Wright and Thom (Reference Wright and Thom1977), which underpins this review and is suitable to address changes typically on the timescales from day to years across hundreds to thousands of metres of coastline.
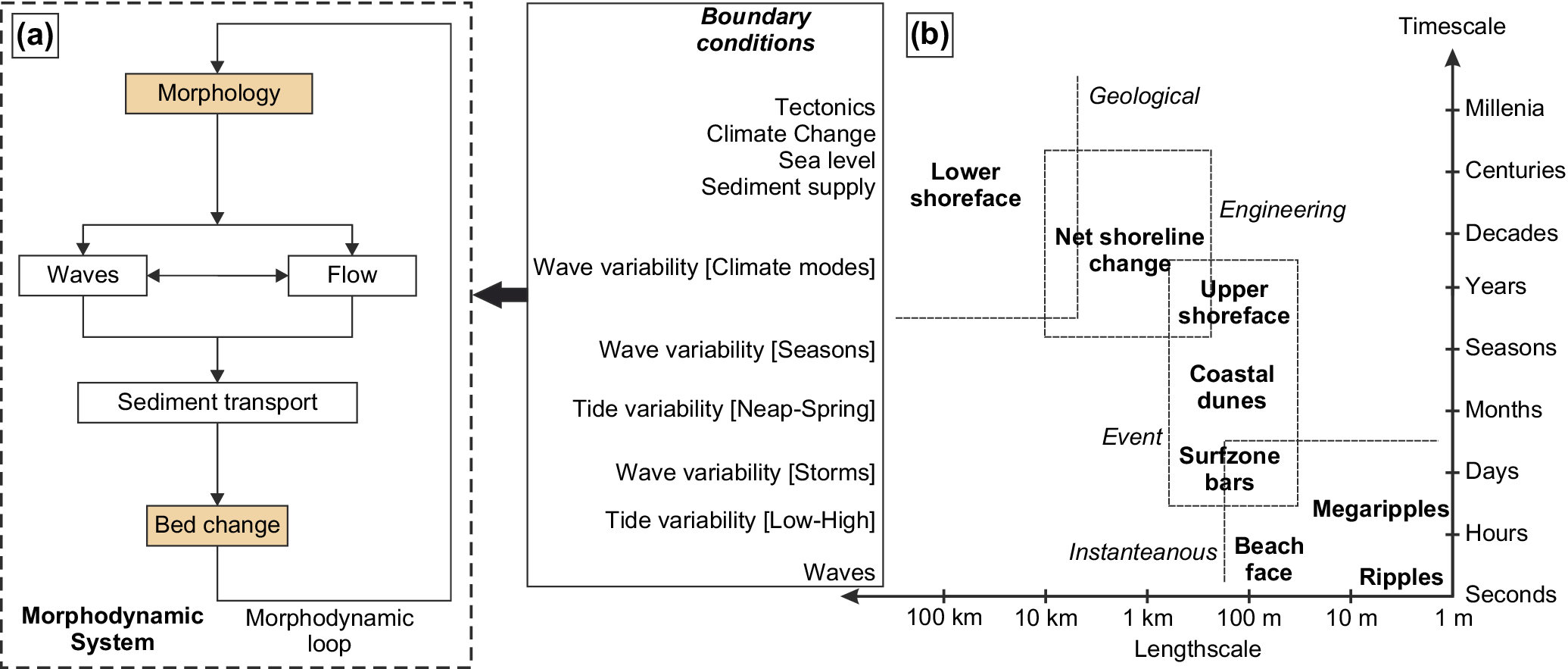
Figure 1. (a) Schematics of the coupled beach morphodynamic system and (b) time–space diagram of the primary modes of sandy beach variability modified after Cowell et al. (Reference Cowell, Thom, van de Plassche, RWG and Woodroffe1995).
The last decades have been characterised by major advances in the understanding and modelling capacity of sandy beach dynamics, building on theoretical work (Ribas et al. Reference Ribas, Falques, de Swart, Dodd, Garnier and Calvete2015), intensive field experiments (Senechal et al. Reference Senechal, Abadie, Gallagher, MacMahan, Masselink, Michallet, Reniers, Ruessink, Russell, Sous, Turner, Ardhuin, Bonneton, Bujan, Capo, Certain, Pedreros and Garlan2011), laboratory experiments (Ruessink et al. Reference Ruessink, Blenkinsopp, Brinkkemper, Castelle, Dubarbier, Grasso, Puleo and Lanckriet2016) and monitoring programmes (Turner et al. Reference Turner, Harley, Short, Simmons, Bracs, Phillips and Splinter2016; Ludka et al. Reference Ludka, Guza, O’Reilly, Merrifield, Flick, Bak, Hesser, Bucciarelli, Olfe, Woodward, Boyd, Smith, Okihiro, Grenzeback, Parry and Boyd2019). Such advances, which have provided new and quantitative insight into the underlying mechanisms underpinning the empirical morphodynamic framework of Wright and Thom (Reference Wright and Thom1977), are included in this review of the morphodynamics of wave-dominated sandy beaches. It is acknowledged that beach morphology and processes are also affected by tides and geological factors, human interventions including coastal structures and beach nourishment, and that beaches can also be composed of gravel or even cobble-sized sediments, but our emphasis is on how ocean waves affect the morphological behaviour of natural sandy beaches. The ‘Nearshore processes’ section provides a brief overview of the key nearshore processes that shape sandy beaches. The ‘Static beach state classification’ section focuses on the spatial variability in beach morphology by describing static beach state classification models. The ‘Beach morphodynamics’ section discusses the underlying processes driving cross-shore and alongshore beach behaviour and, in turn, beach state changes. The ‘Conclusions and future perspectives’ section concludes this review and offers some future perspectives.
Nearshore processes
In the nearshore region, depth-induced gravity wave breaking is the primary driver of nearshore currents, sediment transport and morphological changes (Figure 2). From deep to intermediate water, waves start to ‘feel’ the bottom at water depth
![]() $ h<L/2 $
, where
$ h<L/2 $
, where
![]() $ L $
is the wavelength, and undergo the following changes (Dean and Dalrymple Reference Dean and Dalrymple1991): (1) wave shape becomes asymmetric by developing horizontal and vertical asymmetries (from linear to nonlinear wave theory); (2) onshore mass transport becomes nonzero and (3) waves shoal (increase in height) and refract with decreasing water depth, and can diffract and reflect in the presence of abrupt seabed changes or obstacles. These processes continue until, critically, depth-induced breaking occurs when the ratio of wave height to local water depth reaches the breaker index value
$ L $
is the wavelength, and undergo the following changes (Dean and Dalrymple Reference Dean and Dalrymple1991): (1) wave shape becomes asymmetric by developing horizontal and vertical asymmetries (from linear to nonlinear wave theory); (2) onshore mass transport becomes nonzero and (3) waves shoal (increase in height) and refract with decreasing water depth, and can diffract and reflect in the presence of abrupt seabed changes or obstacles. These processes continue until, critically, depth-induced breaking occurs when the ratio of wave height to local water depth reaches the breaker index value
![]() $ \gamma $
(c. 0.8), which depends on many factors (e.g., beach slope, breaker type, offshore wave steepness and wind direction; Battjes Reference Battjes1974; Smith and Kraus Reference Smith and Kraus1990; Rattanapitikon and Shibaya Reference Rattanapitikon and Shibaya2000; Sous et al. Reference Sous, Forsberg, Touboul and Gonçalves Nogueira2021), before waves run up the beach face in the swash zone (Figure 2). Of note, incident gravity waves exhibit prominent groups that are associated with long ocean waves (Munk Reference Munk1949), known as infragravity waves (Bertin et al. Reference Bertin, de Bakker, van Dongeren, Coco, André, Ardhuin, Bonneton, Bouchette, Castelle, Crawford, Davidson, Deen, Dodet, Guérin, Inch, Leckler, McCall, Muller, Olabarrieta, Roelvink, Ruessink, Sous, Stutzmann and Tissier2018), with frequencies below those of the gravity short waves (generally
$ \gamma $
(c. 0.8), which depends on many factors (e.g., beach slope, breaker type, offshore wave steepness and wind direction; Battjes Reference Battjes1974; Smith and Kraus Reference Smith and Kraus1990; Rattanapitikon and Shibaya Reference Rattanapitikon and Shibaya2000; Sous et al. Reference Sous, Forsberg, Touboul and Gonçalves Nogueira2021), before waves run up the beach face in the swash zone (Figure 2). Of note, incident gravity waves exhibit prominent groups that are associated with long ocean waves (Munk Reference Munk1949), known as infragravity waves (Bertin et al. Reference Bertin, de Bakker, van Dongeren, Coco, André, Ardhuin, Bonneton, Bouchette, Castelle, Crawford, Davidson, Deen, Dodet, Guérin, Inch, Leckler, McCall, Muller, Olabarrieta, Roelvink, Ruessink, Sous, Stutzmann and Tissier2018), with frequencies below those of the gravity short waves (generally
![]() $ < $
0.04–0.05 Hz). On gently sloping beaches under storm conditions, infragravity waves can dominate the inner surf zone (and swash) energy spectra (e.g., Guza and Thornton Reference Guza and Thornton1982; Raubenheimer and Guza Reference Raubenheimer and Guza1996; Ruessink Reference Ruessink1998; Roelvink et al. Reference Roelvink, Reniers, van Dongeren, van Thiel de Vries, McCall and Lescinski2009).
$ < $
0.04–0.05 Hz). On gently sloping beaches under storm conditions, infragravity waves can dominate the inner surf zone (and swash) energy spectra (e.g., Guza and Thornton Reference Guza and Thornton1982; Raubenheimer and Guza Reference Raubenheimer and Guza1996; Ruessink Reference Ruessink1998; Roelvink et al. Reference Roelvink, Reniers, van Dongeren, van Thiel de Vries, McCall and Lescinski2009).
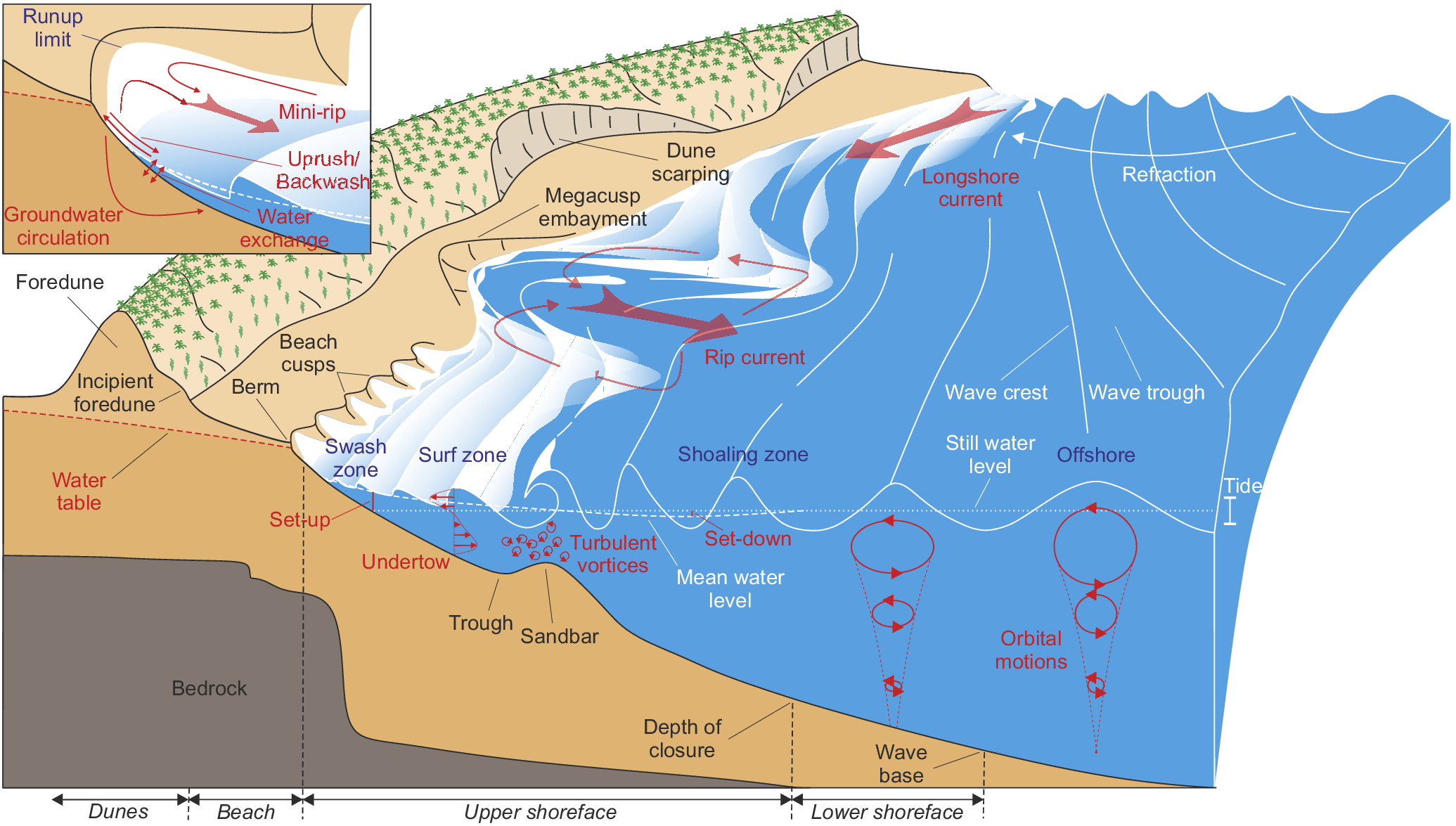
Figure 2. Schematics of the primary hydrodynamic and sediment transport processes occurring on wave-dominated beaches and the primary morphological and hydrodynamics compartments.
Energy loss through depth-induced gravity wave breaking results in a reduction of the wave momentum flux, or radiation stress (Longuet-Higgins and Stewart Reference Longuet-Higgins and Stewart1964), which drives the nearshore circulation system (Svendsen Reference Svendsen2006) consisting of set-up, undertow, longshore currents and rip currents (Figure 2). In short, (1) wave set-up is the increase in mean water level due to wave breaking (Bowen et al. Reference Bowen, Inman and Simmons1968); (2) undertow is a seaward-directed mean current compensating the near-surface net onshore mass flux due to both the organised wave motion and breaking wave roller, with its largest values close to the bottom and (3) rip currents are narrow and seaward-directed jets flowing through the surf zone. On open sandy beaches, the two most common types of rip current are (see the review of Castelle et al. Reference Castelle, Scott, Brander and McCarroll2016): (1) flash rips on alongshore-uniform beaches associated with surf zone eddies, which are transient in both time and space (Johnson and Pattiaratchi Reference Johnson and Pattiaratchi2006; Feddersen Reference Feddersen2014) and (2) channel rips flowing through the incised channels between sand bars (Figure 1), which are fixed in location and driven by alongshore variation in breaking wave energy dissipation due to alongshore variability in water depth (Bowen Reference Bowen1969; Haller et al. Reference Haller, Dalrymple and Svendsen2002; Bruneau et al. Reference Bruneau, Bonneton, Castelle and Pedreros2011).
Bed-load and suspended-load transport modes typically co-exist on sandy beaches (e.g., Komar Reference Komar1978; Bailard and Inman Reference Bailard and Inman1981) with, under high bed shear stresses (e.g., swash zone), sheet flow transport occurring where large quantities of sand are transported in a mixed sand–water layer moving very close to the bed (Masselink and Hughes Reference Masselink and Hughes1998; Lanckriet and Puleo Reference Lanckriet and Puleo2015). Critical to beach morphological response is cross-shore sediment transport. At any point along a beach profile, the net sediment transport is the result of the imbalance between the onshore-directed sediment transport driven by wave nonlinearity (skewed and asymmetric near-bed orbital velocities) and the offshore-directed sediment transport driven by the undertow, with infragravity waves also advecting the suspended sand either onshore or offshore (Osborne and Greenwood Reference Osborne and Greenwood1992; Ruessink et al. Reference Ruessink, Houwman and Hoekstra1998; Smith and Mocke Reference Smith and Mocke2002) depending on the local ratio of gravity and infragravity wave heights (de Bakker et al. Reference de Bakker, Brinkkemper, van der Steen, Tissier and Ruessink2016). During storms, intense wave breaking drives strong undertows that transport sediment seaward, resulting in offshore sandbar migration and beach erosion (e.g., Sallenger et al. Reference Sallenger, Holman and Birkemeier1985; Roelvink and Stive Reference Roelvink and Stive1989; Gallagher et al. Reference Gallagher, Elgar and Guza1998). During weakly to nonbreaking, yet sufficiently energetic, wave conditions, the near-bed wave-nonlinearity-driven bedload transport results in slow onshore sandbar migration concurrent with the accretion of the beach and berm formation (e.g., Trowbridge and Young Reference Trowbridge and Young1989; Gallagher et al. Reference Gallagher, Elgar and Guza1998). The time evolution of the respective contributions of wave nonlinearities and undertow to the net cross-shore sediment transport (Thornton et al. Reference Thornton, Humiston and Birkemeier1996; Hoefel and Elgar Reference Hoefel and Elgar2003), which control beach response, is therefore intrinsically linked with incident wave climate variability (Figure 1b).
All wave-dominated beaches and surf zones are subjected to the same fundamental physical wave processes, but surf zone hydrodynamics differ significantly between steep and gentle beaches (Huntley and Bowen Reference Huntley and Bowen1985). The difference in surf zone characteristics can be quantified by simple nondimensional parameters (Anthony Reference Anthony1998), such as the surf scaling parameter (
![]() $ {\varepsilon}_b $
)
$ {\varepsilon}_b $
)
where
![]() $ {H}_b $
,
$ {H}_b $
,
![]() $ T $
and
$ T $
and
![]() $ \tan \beta $
are significant breaking wave height, wave period and beach slope, respectively. The surf scaling parameter can be used to discriminate between reflective wave conditions with surging breakers and standing wave motion (
$ \tan \beta $
are significant breaking wave height, wave period and beach slope, respectively. The surf scaling parameter can be used to discriminate between reflective wave conditions with surging breakers and standing wave motion (
![]() $ {\varepsilon}_b<2 $
), and dissipative conditions with spilling breakers (
$ {\varepsilon}_b<2 $
), and dissipative conditions with spilling breakers (
![]() $ {\varepsilon}_b>20 $
); intermediate conditions with plunging breakers occur in between.
$ {\varepsilon}_b>20 $
); intermediate conditions with plunging breakers occur in between.
Static beach state classification
Systematic field observations of beach morphological change commenced in the 1950s and, complimented by concurrent wave flume experiments, revealed the highly dynamic nature of beaches. These early studies, summarised by Komar (Reference Komar1976), highlighted the important control of wave conditions. Simple parameterisations of wave conditions (height, energy and steepness), sometimes involving sediment properties, were proposed as onshore/offshore transport thresholds (e.g., Gourlay Reference Gourlay1968; Dean Reference Dean1973). Wave conditions vary over a range of timescales, and beach morphology is expected to vary accordingly (Figure 1), giving rise to the notion of cyclic and seasonal beach response (Nordstrom Reference Nordstrom1980). This understanding resulted in a dichotomised profile characterisation of storm versus post-storm (and winter versus summer, bar versus berm and swell versus sea), and an essential component of the process of transitioning between these two polarised profile configurations is cross-shore bar migration. Furthermore, it became recognised that the transition between ‘barred’ and ‘non-barred’ beach profiles is characterised by Markovian inheritance (Sonu and van Beek Reference Sonu and van Beek1971), whereby any resulting beach profile depends on a preceding profile, and that such transitions generally involve the development of three-dimensional bar features, referred to as ‘rhythmic topography’ (Sonu Reference Sonu1973).
By exploiting the natural laboratory of the southeast coast of New South Wales with its wide range of wave conditions and beaches, Australian coastal researchers were the first to link the variability in beach morphology to surf zone hydrodynamics. Short (Reference Short1979) proposed a beach model based on several years of daily observations on Narrabeen Beach, Sydney, that covered the full reflective–dissipative domain, recognising erosional and accretionary beach state transitions. Wright et al. (Reference Wright, Chappell, Thom, Bradshaw and Cowell1979) developed a similar model based on field measurements of waves and currents on different New South Wales beaches, also covering the full reflective–dissipative spectrum. The Short (Reference Short1979) model was thus based on the temporal changes on a single beach forced by variations in the wave conditions, whereas the approach of Wright et al. (Reference Wright, Chappell, Thom, Bradshaw and Cowell1979) leveraged the spatial variability in environmental conditions (mainly waves and sediments). The models were consolidated in a beach model consisting of six distinctive beach states, including the reflective and dissipative end members, and four intermediate beach states (Wright and Short Reference Wright and Short1984; see Figure 3). Reflective beaches are characterised by a steep beach face and often the presence of a beach step and beach cusps, whereas dissipative beaches have a low-gradient and subdued (multiple) linear bar morphology. The intermediate beach types are all characterised by rhythmic nearshore bar morphology. The real innovation of the Australian beach model was to link the occurrence of different beach types to the dimensionless fall velocity
![]() $ \Omega $
, originally proposed by Gourlay (Reference Gourlay1968) to separate onshore and offshore sediment transport based on flume experiments
$ \Omega $
, originally proposed by Gourlay (Reference Gourlay1968) to separate onshore and offshore sediment transport based on flume experiments
where
![]() $ {w}_s $
is the sediment fall velocity of the beach sediment. The different beach types and their associated values are: reflective (R,
$ {w}_s $
is the sediment fall velocity of the beach sediment. The different beach types and their associated values are: reflective (R,
![]() $ \Omega <1 $
); low tide terrace (LTT,
$ \Omega <1 $
); low tide terrace (LTT,
![]() $ \Omega =2 $
); transverse bar–rip (TBR,
$ \Omega =2 $
); transverse bar–rip (TBR,
![]() $ \Omega =3 $
); rhythmic bar and beach (RBB,
$ \Omega =3 $
); rhythmic bar and beach (RBB,
![]() $ \Omega =4 $
); longshore bar–trough (LBT,
$ \Omega =4 $
); longshore bar–trough (LBT,
![]() $ \Omega =5 $
) and dissipative (D,
$ \Omega =5 $
) and dissipative (D,
![]() $ \Omega >6 $
; Figure 3).
$ \Omega >6 $
; Figure 3).
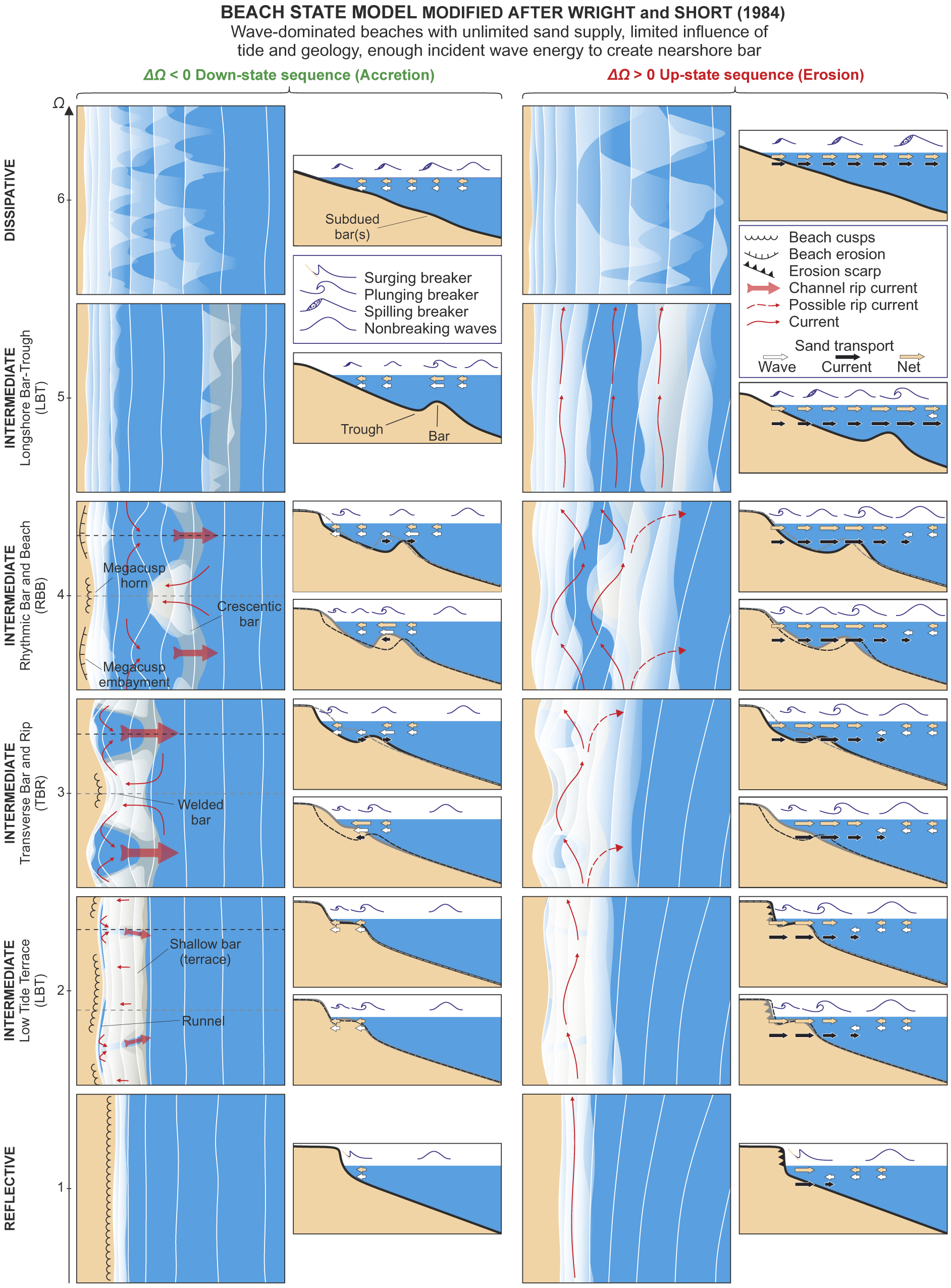
Figure 3. Beach state model modified after Wright and Short (Reference Wright and Short1984) with (left-hand panels) accretive downstate sequences and (right-hand panels) erosive upstate sequences. The arrows represent indicative sediment transport magnitude and direction with relative contributions of waves and currents.
The Australian beach model has been widely used as a basis for further research, and objective classification of beach morphology using video data broadly confirmed the Australian beach types and also enabled the identification of residence times and beach state transitions (Lippmann and Holman Reference Lippmann and Holman1990; Ranasinghe et al. Reference Ranasinghe, Symonds, Black and Holman2004). The distinctive hydrodynamic process signatures that characterise the different beach types in terms of the importance of incident waves, infragravity waves and mean flows identified by Wright and Short (Reference Wright and Short1984) was also further explored (Aagaard et al. Reference Aagaard, Greenwood and Hughes2013; Hughes et al. Reference Hughes, Aagaard, Baldock and Power2014; Figure 3).
Researchers also recognised shortcomings in the model. The role of tides in beach morphodynamics was addressed by Wright et al. (Reference Wright, Nielsen, Short and Green1982, Reference Wright, Short, Boon, Hayden, Kimball and List1987), and Masselink and Short (Reference Masselink and Short1993) introduced an additional dimensionless parameter, the relative tide range RTR, representing the ratio between the mean spring tide range and breaking wave height, to quantify the tidal importance in shaping beach morphology. On beaches with multiple bars, bar dynamics were found to be coupled with the outer bar morphology modulating the wave energy reaching the inner bar system(s) (Senechal et al. Reference Senechal, Gouriou, Castelle, Parisot, Capo, Bujan and Howa2009), resulting in the formulation of multibar models (Short and Aagaard Reference Short and Aagaard1993; Castelle et al. Reference Castelle, Bonneton, Dupuis and Senechal2007). Gravel beaches have a value for
![]() $ \Omega <1 $
even under the most energetic wave conditions; however, distinctive gravel beach types exist that do not readily match the description of the reflective beach type, including pure gravel beaches, mixed sand–gravel beaches and composite gravel beaches (Jennings and Shulmeister Reference Jennings and Shulmeister2002). Application of the beach model, originally developed based on observations on exposed sandy beaches, to low-energy settings proved problematic, most likely due to the presence of absolute energy thresholds to generate certain morphologies (bars and rips). It either led to the identification of unique beach types (Hegge et al. Reference Hegge, Eliot and Hsu1996) or it was found that following high-energy events, the beach morphology can become arrested over extended periods of low-wave conditions (Goodfellow and Stephenson Reference Goodfellow and Stephenson2005; Ojeda et al. Reference Ojeda, Guillén and Ribas2011). The existence of wave energy thresholds also proved to be a critical factor in the classification of UK beaches; Scott et al. (Reference Scott, Masselink and Russell2011) found that a wave energy flux
$ \Omega <1 $
even under the most energetic wave conditions; however, distinctive gravel beach types exist that do not readily match the description of the reflective beach type, including pure gravel beaches, mixed sand–gravel beaches and composite gravel beaches (Jennings and Shulmeister Reference Jennings and Shulmeister2002). Application of the beach model, originally developed based on observations on exposed sandy beaches, to low-energy settings proved problematic, most likely due to the presence of absolute energy thresholds to generate certain morphologies (bars and rips). It either led to the identification of unique beach types (Hegge et al. Reference Hegge, Eliot and Hsu1996) or it was found that following high-energy events, the beach morphology can become arrested over extended periods of low-wave conditions (Goodfellow and Stephenson Reference Goodfellow and Stephenson2005; Ojeda et al. Reference Ojeda, Guillén and Ribas2011). The existence of wave energy thresholds also proved to be a critical factor in the classification of UK beaches; Scott et al. (Reference Scott, Masselink and Russell2011) found that a wave energy flux
![]() $ P $
of 3 kW m
$ P $
of 3 kW m
![]() $ {}^{-1} $
was found to differentiate between intermediate beaches with
$ {}^{-1} $
was found to differentiate between intermediate beaches with
![]() $ (P>3 $
kW m
$ (P>3 $
kW m
![]() $ {}^{-1} $
) and without
$ {}^{-1} $
) and without
![]() $ (P<3 $
kW m
$ (P<3 $
kW m
![]() $ {}^{-1} $
) three-dimensional bar/rip morphology. Geology is generally identified as the most important factor that is missing from the beach model, and it has been argued that for embayed beaches, geological factors are more important determinants of beach morphology than contemporary dynamics (Jackson et al. Reference Jackson, Cooper and Río2005; Loureiro et al. Reference Loureiro, Ferreira, Cooper and Cooper2013). Gallop et al. (Reference Gallop, Kennedy, Loureiro, Naylor, Muñoz-Pérez, Jackson and Fellowes2020) argue that geologically controlled beaches are a distinct beach type, having unique morphodynamics, and McCarroll et al. (Reference McCarroll, Brander, Turner and Leeuwen2016) proposed a new headland-protected beach type that is resistant to upstate transition.
$ {}^{-1} $
) three-dimensional bar/rip morphology. Geology is generally identified as the most important factor that is missing from the beach model, and it has been argued that for embayed beaches, geological factors are more important determinants of beach morphology than contemporary dynamics (Jackson et al. Reference Jackson, Cooper and Río2005; Loureiro et al. Reference Loureiro, Ferreira, Cooper and Cooper2013). Gallop et al. (Reference Gallop, Kennedy, Loureiro, Naylor, Muñoz-Pérez, Jackson and Fellowes2020) argue that geologically controlled beaches are a distinct beach type, having unique morphodynamics, and McCarroll et al. (Reference McCarroll, Brander, Turner and Leeuwen2016) proposed a new headland-protected beach type that is resistant to upstate transition.
The Australian beach model is mainly a static predictive model, but of equal interest is the dynamic beach behaviour, especially the transitions between the different beach types. Such transitions are fundamentally driven by a disequilibrium between the surf zone hydrodynamics and the beach morphology, addressed in the ‘Cross-shore behaviour’ section.
Beach morphodynamics
In the coupled morphodynamic system (Figure 1a), hydrodynamic processes respond instantaneously to morphological change (Wright and Thom Reference Wright and Thom1977). However, morphological change requires the redistribution of sediment, with sediment taking a finite time to move, resulting in a lag in the morphological response to hydrodynamic forcing and a disequilibrium between incident wave conditions and beach morphology (Wright et al. Reference Wright, Short and Green1985). In addition, morphodynamic processes exhibit positive and negative feedback mechanisms driving the development or decay of rhythmic patterns in the sand (‘morphodynamic instabilities’), including sand ripples, beach cusps, transverse bars, crescentic sandbars and capes (Seminara Reference Seminara1998). These concepts of equilibrium beach response and morphodynamic instabilities are key to cross-shore and longshore beach behaviour (see the ‘Cross-shore behaviour’ and ‘Alongshore behaviour’ sections), and can explain the empirical beach state models described in the ‘Static beach state classification’ section, including their dynamic transitions (see the ‘Coupled cross-shore and alongshore behaviour and natural complexity’ section).
Cross-shore behaviour
A fundamental aspect of cross-shore beach profile behaviour is that sediment transport and morphological changes are governed by wave process gradients. In other words, the hydrodynamic driving forces vary in the cross-shore direction (Figure 2), and the resulting gradients in net sediment transport drive morphological change, including the formation, migration and decay of berm and bar features through feedback mechanisms. Process-based beach profile models have shown fair skill in predicting the underwater beach profile evolution at different sites on timescales from hours to years during both moderate and storm conditions (e.g., Thornton et al. Reference Thornton, Humiston and Birkemeier1996; Hoefel and Elgar Reference Hoefel and Elgar2003; Ruessink et al. Reference Ruessink, Kuriyama, Reniers, Roelvink and Walstra2007; Roelvink et al. Reference Roelvink, Reniers, van Dongeren, van Thiel de Vries, McCall and Lescinski2009; Dubarbier et al. Reference Dubarbier, Castelle, Marieu and Ruessink2015). However, these models still require rigorous site-specific calibration. In addition, wave phase-averaged models, which disregard swash sediment transport processes, fail to reproduce the upper beach evolution and berm development. More computationally expensive gravity or infragravity wave phase-resolving models (Roelvink et al. Reference Roelvink, Reniers, van Dongeren, van Thiel de Vries, McCall and Lescinski2009; Briganti et al. Reference Briganti, Torres-Freyermuth, Baldock, Brocchini, Dodd, Hsu, Jiang, Kim, Pintado-Patiño and Postacchini2016) are more appropriate to simulate morphological changes along this section of the beach profile.
Even under steady wave forcing, given the lag in morphological response to hydrodynamic forcing, it takes time for a beach system to reach equilibrium (Grasso et al. Reference Grasso, Michallet, Barthélemy and Certain2009). However, given that the typical timescales associated with changes in incident wave conditions, compounded by tidal variations in the water level, are shorter than the timescales associated with morphological changes, the beach never attains equilibrium. The direction and rate of morphological change (e.g., erosion vs. accretion) of a given morphological state indicator
![]() $ A $
(e.g., shoreline position and beach state) towards a time-varying equilibrium condition
$ A $
(e.g., shoreline position and beach state) towards a time-varying equilibrium condition
![]() $ {D}_{eq} $
(with
$ {D}_{eq} $
(with
![]() $ D $
, e.g., incident wave energy,
$ D $
, e.g., incident wave energy,
![]() $ \Omega $
) can thus be predicted in terms of the instantaneous wave thrust
$ \Omega $
) can thus be predicted in terms of the instantaneous wave thrust
![]() $ F $
(e.g., wave power or some other wave-based parameter) available to move the sediment, and the dynamic disequilibrium
$ F $
(e.g., wave power or some other wave-based parameter) available to move the sediment, and the dynamic disequilibrium
![]() $ \Delta D=D-{D}_{eq} $
. Equilibrium models are generally of the form
$ \Delta D=D-{D}_{eq} $
. Equilibrium models are generally of the form
with
![]() $ {k}^{+/-} $
a model-free response rate parameter that has different values for accretion (
$ {k}^{+/-} $
a model-free response rate parameter that has different values for accretion (
![]() $ \Delta D<0 $
) and erosion (
$ \Delta D<0 $
) and erosion (
![]() $ \Delta D>0 $
) events. Such equilibrium response was first introduced conceptually by Wright and Short (Reference Wright and Short1984) to describe the beach state transition (with
$ \Delta D>0 $
) events. Such equilibrium response was first introduced conceptually by Wright and Short (Reference Wright and Short1984) to describe the beach state transition (with
![]() $ A $
the beach state and
$ A $
the beach state and
![]() $ F=D=\Omega $
; see Figure 4). Such equilibrium approach was subsequently implemented in simple numerical models (e.g., Miller and Dean Reference Miller and Dean2004; Davidson and Turner Reference Davidson and Turner2009; Davidson et al. Reference Davidson, Lewis and Turner2010) for different morphological descriptors
$ F=D=\Omega $
; see Figure 4). Such equilibrium approach was subsequently implemented in simple numerical models (e.g., Miller and Dean Reference Miller and Dean2004; Davidson and Turner Reference Davidson and Turner2009; Davidson et al. Reference Davidson, Lewis and Turner2010) for different morphological descriptors
![]() $ A $
, such as sandbar cross-shore position (Plant et al. Reference Plant, Holman, Freilich and Birkemeier1999), beach profiles (Larson and Kraus Reference Larson and Kraus1989), sediment grain size (Prodger et al. Reference Prodger, Russell, Davidson, Miles and Scott2016), three-dimensional beach morphology (Stokes et al. Reference Stokes, Davidson and Russell2015), coastal embayment rotation (Turki et al. Reference Turki, Medina, Coco and González2013) and, mostly, shoreline
$ A $
, such as sandbar cross-shore position (Plant et al. Reference Plant, Holman, Freilich and Birkemeier1999), beach profiles (Larson and Kraus Reference Larson and Kraus1989), sediment grain size (Prodger et al. Reference Prodger, Russell, Davidson, Miles and Scott2016), three-dimensional beach morphology (Stokes et al. Reference Stokes, Davidson and Russell2015), coastal embayment rotation (Turki et al. Reference Turki, Medina, Coco and González2013) and, mostly, shoreline
![]() $ S $
response from the timescales of hours (storm) to decades at cross-shore transport dominated sites (e.g., Yates et al. Reference Yates, Guza and O’Reilly2009; Davidson et al. Reference Davidson, Splinter and Turner2013; Lemos et al. Reference Lemos, Floc’h, Yates, Dantec, Marieu, Hamon, Cuq, Suanez and Delacourt2018; Jaramillo et al. Reference Jaramillo, Jara, González and Medina2020; D’Anna et al. Reference D’Anna, Castelle, Idier, Rohmer, Cozannet, Thieblemont and Bricheno2021). In the ShoreFor model (Davidson et al. Reference Davidson, Splinter and Turner2013), the disequilibrium condition is based on the weighted average of
$ S $
response from the timescales of hours (storm) to decades at cross-shore transport dominated sites (e.g., Yates et al. Reference Yates, Guza and O’Reilly2009; Davidson et al. Reference Davidson, Splinter and Turner2013; Lemos et al. Reference Lemos, Floc’h, Yates, Dantec, Marieu, Hamon, Cuq, Suanez and Delacourt2018; Jaramillo et al. Reference Jaramillo, Jara, González and Medina2020; D’Anna et al. Reference D’Anna, Castelle, Idier, Rohmer, Cozannet, Thieblemont and Bricheno2021). In the ShoreFor model (Davidson et al. Reference Davidson, Splinter and Turner2013), the disequilibrium condition is based on the weighted average of
![]() $ \Omega $
over the past 2Φ days, attributing to
$ \Omega $
over the past 2Φ days, attributing to
![]() $ \Phi $
the role of beach ‘memory’. Model-free parameters including
$ \Phi $
the role of beach ‘memory’. Model-free parameters including
![]() $ \Phi $
can be estimated based on a weighted mean dimensionless fall velocity accounting for the seasonality in incident wave conditions (Splinter et al. Reference Splinter, Turner, Davidson, Barnard, Castelle and Oltman-Shay2014), resulting in a large inter-site variability of response modes. These contrasting beach responses are qualitatively illustrated in Figure 5, which shows four representative coastal sites with different wave climates (Figure 5a–c) and shoreline response time series: (1) strong seasonal and interannual timescales (large
$ \Phi $
can be estimated based on a weighted mean dimensionless fall velocity accounting for the seasonality in incident wave conditions (Splinter et al. Reference Splinter, Turner, Davidson, Barnard, Castelle and Oltman-Shay2014), resulting in a large inter-site variability of response modes. These contrasting beach responses are qualitatively illustrated in Figure 5, which shows four representative coastal sites with different wave climates (Figure 5a–c) and shoreline response time series: (1) strong seasonal and interannual timescales (large
![]() $ \Phi $
) in southwest France (Figure 5d,f); (2) storm timescale (low
$ \Phi $
) in southwest France (Figure 5d,f); (2) storm timescale (low
![]() $ \Phi $
) in the Mediterranean Sea (Figure 5e,g); (3) (semi-)annual timescale in the Caribbean Sea (Figure 5h,j) and (4) low-amplitude seasonal timescale in the Bight of Benin (Figure 5i,k).
$ \Phi $
) in the Mediterranean Sea (Figure 5e,g); (3) (semi-)annual timescale in the Caribbean Sea (Figure 5h,j) and (4) low-amplitude seasonal timescale in the Bight of Benin (Figure 5i,k).
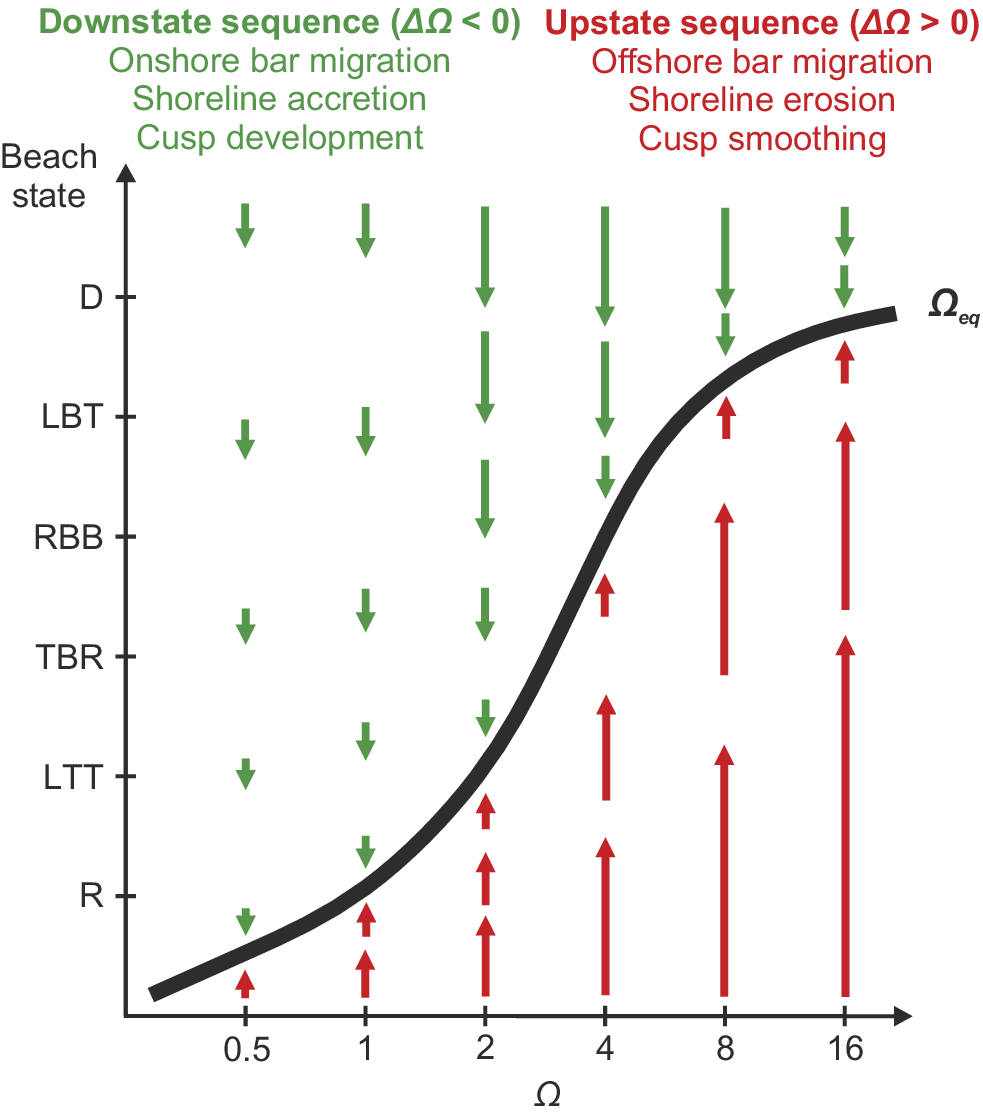
Figure 4. Conceptual diagram illustrating the relationships between change in beach state (and bar migration, shoreline change and cusp development) and morphodynamic disequilibrium and incident wave thrust, with arrow length proportional to the rate of change. Modified after Wright and Short (Reference Wright and Short1984).
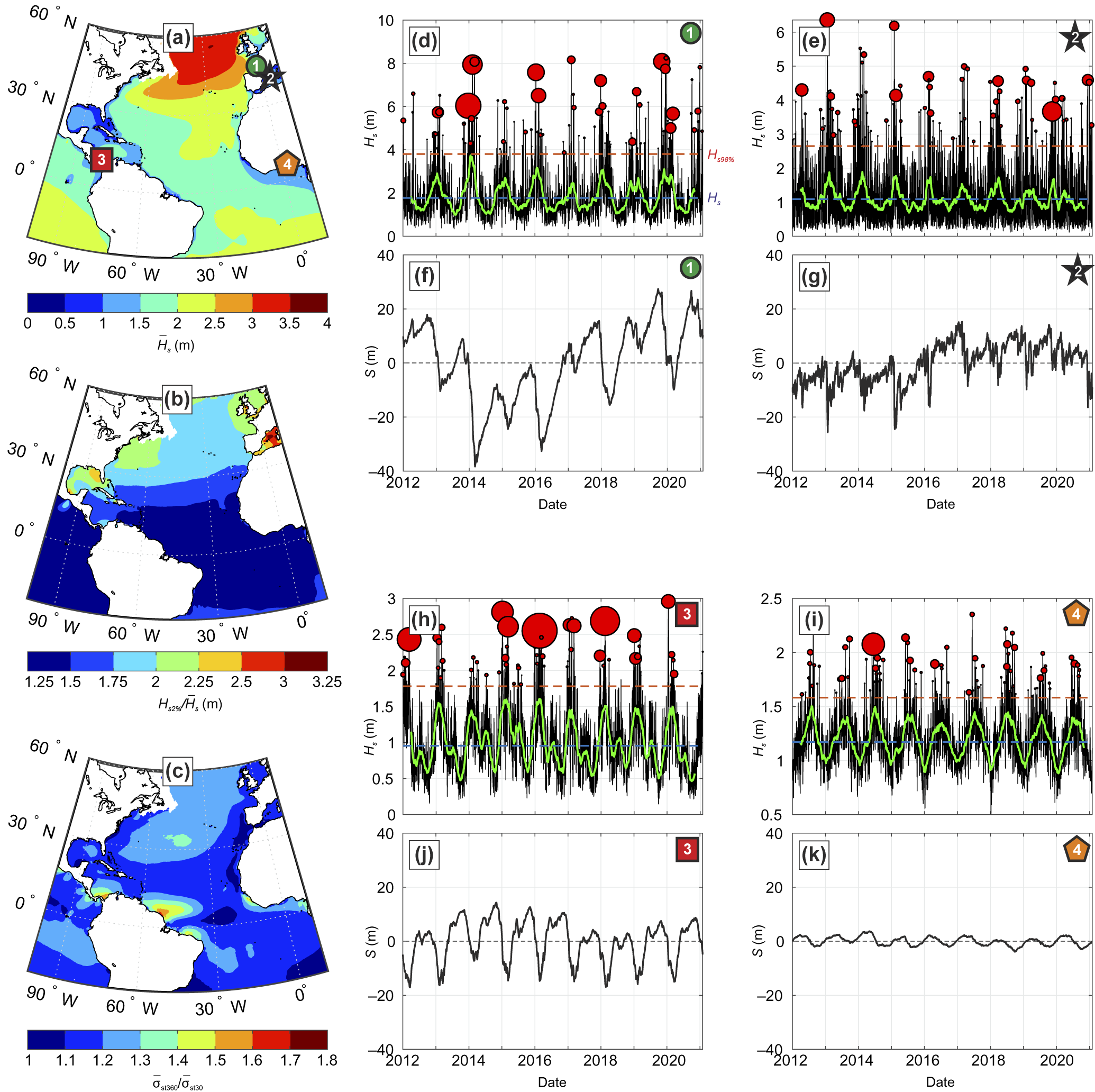
Figure 5. Illustration of the range of timescales and amplitude of beach response, here looking at shoreline position
![]() $ S $
. Left-hand panels: spatial distribution of (a) mean significant wave height
$ S $
. Left-hand panels: spatial distribution of (a) mean significant wave height
![]() $ {\overline{H}}_s $
, (b)
$ {\overline{H}}_s $
, (b)
![]() $ {H}_{s95\%}/{\overline{H}}_s $
where
$ {H}_{s95\%}/{\overline{H}}_s $
where
![]() $ {H}_{s95\%} $
is the 0.95 quantile and (c)
$ {H}_{s95\%} $
is the 0.95 quantile and (c)
![]() $ {\overline{\sigma}}_{H/T360}/{\overline{\sigma}}_{H/T30} $
where
$ {\overline{\sigma}}_{H/T360}/{\overline{\sigma}}_{H/T30} $
where
![]() $ {\overline{\sigma}}_{H/T30} $
(
$ {\overline{\sigma}}_{H/T30} $
(
![]() $ {\overline{\sigma}}_{H/T360} $
) is the average standard deviation of
$ {\overline{\sigma}}_{H/T360} $
) is the average standard deviation of
![]() $ {H}_s/{T}_p $
at the monthly (yearly) timescale. Right-hand panels: time series of (d,e,h,i)
$ {H}_s/{T}_p $
at the monthly (yearly) timescale. Right-hand panels: time series of (d,e,h,i)
![]() $ {H}_s $
(black), its 2-month moving averaged (thick green) and storms (bubbles) with bubble size proportional to storm duration according to Masselink et al. (Reference Masselink, Austin, Scott, Poate and Russell2014), with the largest bubble in (h) corresponding to a 27.25-day cluster, and (f,g,j,k) of shoreline position deviation around the mean S modelled with an adaptation of the ShoreFor model. The locations of the four sites are shown in (a). A first-pass calibration was performed for sites (d,f) and (i,k), and arbitrary parameters were used at (e,g) and (h,j).
$ {H}_s $
(black), its 2-month moving averaged (thick green) and storms (bubbles) with bubble size proportional to storm duration according to Masselink et al. (Reference Masselink, Austin, Scott, Poate and Russell2014), with the largest bubble in (h) corresponding to a 27.25-day cluster, and (f,g,j,k) of shoreline position deviation around the mean S modelled with an adaptation of the ShoreFor model. The locations of the four sites are shown in (a). A first-pass calibration was performed for sites (d,f) and (i,k), and arbitrary parameters were used at (e,g) and (h,j).
Alongshore behaviour
In contrast with cross-shore behaviour, alongshore behaviour on open sandy beaches is characterised by no process gradients as offshore wave conditions are mostly uniform alongshore. Despite this (initial) alongshore uniformity in wave forcing, the nearshore region often exhibits a wide range of coherent patterns in the sand, such as beach cusps (tens of metres; Guza and Inman Reference Guza and Inman1975; Coco et al. Reference Coco, O’Hare and Huntley1999), megacusps (hundreds of metres; Short Reference Short1999; Thornton et al. Reference Thornton, MacMahan and Sallenger2007; Castelle et al. Reference Castelle, Marieu, Bujan, Splinter, Robinet, Sénéchal and Ferreira2015) and three-dimensional surf zone bars (tens to thousands of metres; Short Reference Short1999; van Enckevort et al. Reference van Enckevort, Ruessink, Coco, Suzuki, Turner, Plant and Holman2004), as shown in Figure 3. The formation of these rhythmic features was initially ascribed to a forcing template in the hydrodynamics (Bowen and Inman Reference Bowen and Inman1971; Guza and Inman Reference Guza and Inman1975; Holman and Bowen Reference Holman and Bowen1982), namely standing edge waves, which are alongshore periodic infragravity waves trapped close to the shoreline by refraction and reflection (Guza and Davis Reference Guza and Davis1974). Similarly, cross-shore standing infragravity waves have been considered responsible for multiple nearshore parallel bars (Bowen Reference Bowen and McCann1980).
Such ‘forcing template’ theories for generating rhythmic patterns on beaches have been superseded by new explanations involving interactions between fluid flow, sediment transport and evolving morphology that create positive feedback mechanisms and lead to spontaneous pattern self-organisation (see the review of Coco and Murray Reference Coco and Murray2007). Flow over a mobile bed, through associated sediment fluxes, can reshape the bed. If the changes in the shape of the bed reinforce the patterns of flow and sediment fluxes that lead to the shape change (positive feedback), finite-amplitude bed features (‘morphodynamic instabilities’) can rapidly emerge where no coherent flow or sediment structures previously existed. Morphodynamic instabilities, which have been successfully modelled through linear or nonlinear stability analyses (e.g., Deigaard et al. Reference Deigaard, Drønen, Fredsøe, Jensen and Jorgensen1999; Falqués et al. Reference Falqués, Coco and Huntley2000; Calvete et al. Reference Calvete, Dodd, Falqués and van Leeuwen2005; Falqués et al. Reference Falqués, Dodd, Garnier, Ribas, MacHardy, Larroudé, Calvete and Sancho2008; Castelle and Ruessink Reference Castelle and Ruessink2011) typically take the form of an alongshore sequence of horns (shoals) and bays (cross-shore troughs), alternating shoreward and seaward of a shore-parallel line (van Enckevort et al. Reference van Enckevort, Ruessink, Coco, Suzuki, Turner, Plant and Holman2004). They can form through different feedback mechanisms. For example, crescentic bars, finger bars and beach cusps develop through bed–surf (Falqués et al. Reference Falqués, Coco and Huntley2000), bed–flow (Ribas and Kroon Reference Ribas and Kroon2007) and beach–swash (Werner and Fink Reference Werner and Fink1993) interactions, respectively. Under time-invariant wave forcing, these instabilities self-organise into alongshore-uniform features through merging and splitting (Garnier et al. Reference Garnier, Calvete, Falqués and Caballeria2006).
Coupled cross-shore and alongshore behaviour and natural complexity
The development of morphodynamic instabilities has been mostly observed during down-state (accretive) sequences (see the ‘Static beach state classification’ section), corresponding to a positive disequilibrium
![]() $ (\Delta D<0 $
; see the ‘Cross-shore behaviour’ section) characterised by general onshore sediment transport. From an initially alongshore-uniform offshore sandbar (e.g., LBT state), surf zone morphodynamic instabilities can develop through positive feedback between wave-driven rip-cell circulation and the evolving seabed (bed–surf interaction; Falqués et al. Reference Falqués, Coco and Huntley2000). Dubarbier et al. (Reference Dubarbier, Castelle, Ruessink and Marieu2017) performed the first numerical experiment of a full down-state sequence from LBT to LTT. They showed that initially (LBT–RBB–TBR transition), onshore sediment transport driven by wave nonlinearities is critical to the overall rapid onshore sandbar migration (large positive disequilibrium), with concurrent positive feedback mechanisms through bed–surf interaction (alongshore morphodynamic instabilities). During such transition, instability wave length typically decreases through mergings (Garnier et al. Reference Garnier, Dodd, Falqués and Calvete2010) as rip spacing decreases with decreasing sandbar distance to the shore (Calvete et al. Reference Calvete, Dodd, Falqués and van Leeuwen2005). Subsequently (TBR–LTT transition), gravitational downslope sediment transport acts as a damping term inhibiting further channel growth enforced by rip flow circulation, which, together with the slow onshore sandbar migration (small positive disequilibrium), results in the complete bar welding to the beach and rip channel infilling (negative feedback mechanism), resulting in a relatively alongshore uniform LTT state. In contrast, beach cusps experience positive feedback (bed–swash interaction; Coco et al. Reference Coco, O’Hare and Huntley1999, Coco et al. Reference Coco, Burnet, Werner and Elgar2004) throughout the downstate sequence as evidenced by the increasingly cusped LTT beach face (Figure 3). Up-state (erosive) transitions characterised by general offshore sediment transport are less understood. The rapid decay of these morphodynamic instabilities has been observed during storms together with offshore bar migration (Wright and Short Reference Wright and Short1984; Almar et al. Reference Almar, Castelle, Ruessink, Senechal, Bonneton and Marieu2010). However, under storm conditions with long peak period and shore-normal incidence, morphodynamic instabilities can be maintained and beach megacusp embayments can even erode back to the dune system causing severe localised dune scarping without any up-state sequence (Castelle et al. Reference Castelle, Marieu, Bujan, Splinter, Robinet, Sénéchal and Ferreira2015). More recently, morphodynamic instability decay has been observed and modelled under moderate energy obliquely incident waves (Price and Ruessink Reference Price and Ruessink2011; Garnier et al. Reference Garnier, Falqués, Calvete, Thiébot and Ribas2013), coinciding with dominant offshore sediment transport, large longshore sediment fluxes, beach erosion and seaward sandbar migration (Price and Ruessink Reference Price and Ruessink2011; Walstra et al. Reference Walstra, Reniers, Ranasinghe, Roelvink and Ruessink2012), highlighting the key role of the angle of incidence in up-state sequences (Figure 3).
$ (\Delta D<0 $
; see the ‘Cross-shore behaviour’ section) characterised by general onshore sediment transport. From an initially alongshore-uniform offshore sandbar (e.g., LBT state), surf zone morphodynamic instabilities can develop through positive feedback between wave-driven rip-cell circulation and the evolving seabed (bed–surf interaction; Falqués et al. Reference Falqués, Coco and Huntley2000). Dubarbier et al. (Reference Dubarbier, Castelle, Ruessink and Marieu2017) performed the first numerical experiment of a full down-state sequence from LBT to LTT. They showed that initially (LBT–RBB–TBR transition), onshore sediment transport driven by wave nonlinearities is critical to the overall rapid onshore sandbar migration (large positive disequilibrium), with concurrent positive feedback mechanisms through bed–surf interaction (alongshore morphodynamic instabilities). During such transition, instability wave length typically decreases through mergings (Garnier et al. Reference Garnier, Dodd, Falqués and Calvete2010) as rip spacing decreases with decreasing sandbar distance to the shore (Calvete et al. Reference Calvete, Dodd, Falqués and van Leeuwen2005). Subsequently (TBR–LTT transition), gravitational downslope sediment transport acts as a damping term inhibiting further channel growth enforced by rip flow circulation, which, together with the slow onshore sandbar migration (small positive disequilibrium), results in the complete bar welding to the beach and rip channel infilling (negative feedback mechanism), resulting in a relatively alongshore uniform LTT state. In contrast, beach cusps experience positive feedback (bed–swash interaction; Coco et al. Reference Coco, O’Hare and Huntley1999, Coco et al. Reference Coco, Burnet, Werner and Elgar2004) throughout the downstate sequence as evidenced by the increasingly cusped LTT beach face (Figure 3). Up-state (erosive) transitions characterised by general offshore sediment transport are less understood. The rapid decay of these morphodynamic instabilities has been observed during storms together with offshore bar migration (Wright and Short Reference Wright and Short1984; Almar et al. Reference Almar, Castelle, Ruessink, Senechal, Bonneton and Marieu2010). However, under storm conditions with long peak period and shore-normal incidence, morphodynamic instabilities can be maintained and beach megacusp embayments can even erode back to the dune system causing severe localised dune scarping without any up-state sequence (Castelle et al. Reference Castelle, Marieu, Bujan, Splinter, Robinet, Sénéchal and Ferreira2015). More recently, morphodynamic instability decay has been observed and modelled under moderate energy obliquely incident waves (Price and Ruessink Reference Price and Ruessink2011; Garnier et al. Reference Garnier, Falqués, Calvete, Thiébot and Ribas2013), coinciding with dominant offshore sediment transport, large longshore sediment fluxes, beach erosion and seaward sandbar migration (Price and Ruessink Reference Price and Ruessink2011; Walstra et al. Reference Walstra, Reniers, Ranasinghe, Roelvink and Ruessink2012), highlighting the key role of the angle of incidence in up-state sequences (Figure 3).
As acknowledged by Coco and Murray (Reference Coco and Murray2007), self-organisation hypotheses can be compatible with some template theory concepts. A salient example is morphological coupling whereby offshore bathymetric variability (e.g., outer sandbar and inner shelf ridges), which enforces alongshore variable incident wave conditions, can control the alongshore variability of bar patterns (Castelle et al. Reference Castelle, Ruessink, Bonneton, Marieu, Bruneau and Price2010; Price et al. Reference Price, Ruessink and Castelle2014; Coco et al. Reference Coco, Calvete, Ribas, de Swart and Falqués2020; Nnafie et al. Reference Nnafie, de Swart, Falqués and Calvete2021). Surf zone morphodynamic instabilities are also often mirrored at the shoreline with the presence of megacusp embayments, with megacusp embayments facing rip channels incising the bars (Figure 2). Hydrodynamic templates (edge waves; Guza and Davis Reference Guza and Davis1974) were also found to trigger surf zone morphodynamic instabilities and to affect their fully developed characteristics (Reniers et al. Reference Reniers, Roelvink and Thornton2004). Thus, the role of hydrodynamic templates in generating rhythmic morphology must not be completely excluded.
Conclusions and future perspectives
Using the morphodynamics approach (cf. Figure 1; Wright and Thom Reference Wright and Thom1977) as the underpinning framework, this review provides a synthesis of how ocean waves affect the morphological behaviour of wave-dominated beaches over short-to-medium timescales (days to years). Based primarily on research conducted on relatively energetic
![]() $ ({H}_s>0.25-0.5 $
m) and small tidal (mean spring tide range
$ ({H}_s>0.25-0.5 $
m) and small tidal (mean spring tide range
![]() $ < $
3 m) beaches with abundant sand, the ‘Australian beach model’ (cf. Figure 3; Wright and Short Reference Wright and Short1984) describes the occurrence of beach types across the full reflective–dissipative spectrum based solely on wave conditions and sediment characteristics. The model has been widely tested and applied, and remains a useful physical framework to consider sandy beach morphological characteristics and surf zone hydrodynamics, with significant applications to other fields of research (e.g., beach ecology, surf zone hazards and pollutant dispersal). Transitions between different beach types are driven by temporal changes in the wave forcing conditions, and the wave climate is key in explaining the frequency-response characteristics of beach morphological time series (e.g., beach type, shoreline position and beach volume; cf. Figure 5). Cross-shore morphological changes are primarily controlled by equilibrium principles with below (above) average wave conditions driving down-state (up-state) transitions associated with net onshore (offshore) sediment transport (cf. Figure 5; Davidson et al. Reference Davidson, Splinter and Turner2013). Morphodynamic feedback processes resulting in self-organising behaviour are primarily responsible for alongshore morphological variability and the generation of rhythmic shoreline features, such as crescentic bars, rip channels and beach cusps (Coco and Murray Reference Coco and Murray2007).
$ < $
3 m) beaches with abundant sand, the ‘Australian beach model’ (cf. Figure 3; Wright and Short Reference Wright and Short1984) describes the occurrence of beach types across the full reflective–dissipative spectrum based solely on wave conditions and sediment characteristics. The model has been widely tested and applied, and remains a useful physical framework to consider sandy beach morphological characteristics and surf zone hydrodynamics, with significant applications to other fields of research (e.g., beach ecology, surf zone hazards and pollutant dispersal). Transitions between different beach types are driven by temporal changes in the wave forcing conditions, and the wave climate is key in explaining the frequency-response characteristics of beach morphological time series (e.g., beach type, shoreline position and beach volume; cf. Figure 5). Cross-shore morphological changes are primarily controlled by equilibrium principles with below (above) average wave conditions driving down-state (up-state) transitions associated with net onshore (offshore) sediment transport (cf. Figure 5; Davidson et al. Reference Davidson, Splinter and Turner2013). Morphodynamic feedback processes resulting in self-organising behaviour are primarily responsible for alongshore morphological variability and the generation of rhythmic shoreline features, such as crescentic bars, rip channels and beach cusps (Coco and Murray Reference Coco and Murray2007).
Previous beach research has mainly focused on the relatively easily accessible subaerial beach and the shallow subtidal region, with data obtained using conventional surveys and video imagery. Such data sets are generally not collected at the temporal scale (<10 years) and resolution (monthly) commensurate with beach morphodynamics, which can change from day to day (e.g., during storms; Almar et al. Reference Almar, Castelle, Ruessink, Senechal, Bonneton and Marieu2010) and can display decadal variability due to hemispheric-scale fluctuations in the wave climate (e.g., Masselink et al. Reference Masselink, Austin, Scott, Poate and Russell2014; Barnard et al. Reference Barnard, Hoover, Hubbard, Snyder, Ludka, Allan, Kaminsky, Ruggiero, Gallien, Gabel, McCandless, Weiner, Cohn, Anderson and Serafin2017; Dodet et al. Reference Dodet, Castelle, Masselink, Scott, Davidson, Floc’h, Jackson and Suanez2018). Global satellite data sets going back to the 1980s are beginning to be analysed to explore hemispheric-scale climate forcing of beach change (Vos et al. Reference Vos, Harley, Turner and Splinter2022), and the availability of high-resolution geostationary satellite data also opens new perspectives by increasing data frequency and reducing satellite-derived product uncertainties. The development of advanced nonlinear depth-inversion methods from LiDAR scanners (Martins et al. Reference Martins, Blenkinsopp, Power, Bruder, Puleo and Bergsma2017), X-Band radar or even conventional video monitoring systems (Rutten et al. Reference Rutten, de Jong and Ruessink2017) should enable including changes in the subtidal zone where data are lacking, particularly under energetic wave conditions.
It is increasingly realised that sediment exchange between the upper and lower parts of the shoreface, and also across the depth of closure (cf. Figure 2), can play a key role in the nearshore sediment budget and, thus, beach morphology (Harley et al. Reference Harley, Masselink, de Alegría-Arzaburu, Valiente and Scott2022). These sediment exchanges are difficult to quantify as the associated bed-level changes are comparable to the detection limit. Furthermore, in situ sediment flux measurements require large numbers of state-of-the-art acoustic instruments (e.g., Zedel et al. Reference Zedel, Hay, Wilson and Hare2021) deployed for long periods of time to provide robust information from which to derive a sediment budget. Information gathered with sediment tracers might provide complimentary data (Pearson et al. Reference Pearson, van Prooijen, Poleykett, Wright, Black and Wang2021), especially if co-collected with hydrodynamic data and complimented by numerical modelling.
Complex process-based models, which typically couple hydrodynamics, waves, sediment transport and morphology through mass and momentum conservation laws (Lesser et al. Reference Lesser, Roelvink, van Kester and Stelling2004), are skilful on short temporal (O [days]) and spatial scales (O [100 m]). However, presently these models are not able to adequately simulate the swash–surf–shoaling morphodynamics continuum, and their strongly nonlinear nature results in an inescapable build-up of errors in longer-term simulations. Further progress must be made in the 3D description of nearshore currents, cross-shore sediment transport and beach recovery processes (e.g., Hoefel and Elgar Reference Hoefel and Elgar2003; Uchiyama et al. Reference Uchiyama, McWilliams and Shchepetkin2010). Computationally cheap hybrid models, which are based on general principles (e.g., behavioural laws and semi-empirical rules) and a selection of the dominant driving processes (e.g., cross-shore transport through equilibrium-based response), can lead to more reliable long-term evolution simulations with many recent skilful shoreline applications (Vitousek et al. Reference Vitousek, Barnard, Limber, Erikson and Cole2017; Robinet et al. Reference Robinet, Idier, Castelle and Marieu2018; Antolínez et al. Reference Antolínez, Méndez, Anderson, Ruggiero and Kaminsky2019). These models rely on free parameters that show a variability on timescales of years linked with wave climate variability which needs further investigation (Ibaceta et al. Reference Ibaceta, Splinter, Harley and Turner2020). Sea-level-rise beach response is generally implemented using basic rules (Bruun Reference Bruun1962). New rules-based shoreface translation frameworks, including, for example, dune encroachment or barrier rollback (McCarroll et al. Reference McCarroll, Masselink, Valiente, Scott, Wiggins, Kirby and Davidson2021), must be implemented. Given the uncertainties in the shoreline drivers (e.g., wave climate and sea-level rise) and in shoreline model formulation (e.g., model-free parameters), a (probabilistic) ensemble approach based on such hybrid models must be developed (Montaño et al. Reference Montaño, Coco, Antolínez, Beuzen, Bryan, Cagigal, Castelle, Davidson, Goldstein, Ibaceta, Idier, Ludka, Masoud-Ansari, Méndez, Murray, Plant, Ratliff, Robinet, Rueda, Senechal, Simmons, Splinter, Stephens, Townend, Vitousek and Vos2020; D’Anna et al. Reference D’Anna, Castelle, Idier, Rohmer, Cozannet, Thieblemont and Bricheno2021) to address the future of beaches in the frame of climate change (Vousdoukas et al. Reference Vousdoukas, Ranasinghe, Mentaschi, Plomaritis, Athanasiou, Luijendijk and Feyen2020; Cooper et al. Reference Cooper, Masselink, Coco, Short, Castelle, Rogers, Anthony, Green, Kelley, Pilkey and Jackson2020). Coastal scientists, managers and engineers will thus need to embrace uncertainties and build on improved beach change models to develop coastal management strategies (e.g., beach nourishment, nature-based solutions and well-designed coastal structures) to optimise coastal resilience.
The challenges presented by measuring (and modelling) the highly dynamic beach environments, occasionally exposed to wave conditions in excess of 5 m, require large research efforts, including long-term monitoring programmes (Turner et al. Reference Turner, Harley, Short, Simmons, Bracs, Phillips and Splinter2016), intense field campaigns (Senechal et al. Reference Senechal, Abadie, Gallagher, MacMahan, Masselink, Michallet, Reniers, Ruessink, Russell, Sous, Turner, Ardhuin, Bonneton, Bujan, Capo, Certain, Pedreros and Garlan2011) and mining of remotely sensed data (Vos et al. Reference Vos, Harley, Splinter, Simmons and Turner2019). Such projects, which ideally involve multidisciplinary research teams with expertise in field research, remote sensing, big-data and numerical modelling, will improve our understanding and capacity to predict the future of sandy beaches, trajectory shifts and coastal hazards in an increasingly stormy world.
Open Peer Review
To view the open peer review materials for this article, please visit http://doi.org/10.1017/cft.2022.2.
Data availability statement
Data availability is not applicable to this article as no new data were created or analysed in this study.
Acknowledgements
We thank the Australian researchers who first developed the beach morphodynamic framework and colleagues from all over the world who, over the last decades, have greatly contributed to improve the understanding and modelling capacity of wave-dominated sandy beaches.
Author contributions
Both authors designed the review paper content and drafted the manuscript. B.C. drafted the figures. Both authors revised and edited the text and figures.
Financial support
B.C. was funded by an Agence Nationale de la Recherche grant (ANR-21-CE01-0015). G.M. was funded by an EPSRC Overseas Travel Grant (EP/T004304/1) and by an NERC Strategic Highlight Topics grant (NE/N015525/1).
Competing interests
The authors declare no competing interests exist.


















Comments
Dear Coastal Futrues Editor,
We hereby submit the review "Morphodynamics of wave-dominated beaches" commissioned to your journal,
Sincerely yours,
Bruno Castelle and Gerd Masselink