Research Article
Approximate methods for modelling cavitation bubbles near boundaries
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 1-44
-
- Article
-
- You have access
- Export citation
Optimality conditions for systems with insufficient data
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 45-56
-
- Article
-
- You have access
- Export citation
A unified approach to continuous and certain non-continuous functions II
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 57-74
-
- Article
-
- You have access
- Export citation
Continuous and numerical analysis of a boundary shock problem
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 75-86
-
- Article
-
- You have access
- Export citation
Relatively congruence distributive subquasivarieties of a congruence modular variety
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 87-96
-
- Article
-
- You have access
- Export citation
On the minimum number of blocks defining a design
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 97-112
-
- Article
-
- You have access
- Export citation
On the structure of a real crossed group algebra
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 113-115
-
- Article
-
- You have access
- Export citation
Note on the extensions of Butler groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 117-122
-
- Article
-
- You have access
- Export citation
A Hilbert algebra of Hilbert-Schmidt quadratic operators
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 123-134
-
- Article
-
- You have access
- Export citation
Slant immersions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 135-147
-
- Article
-
- You have access
- Export citation
Mordell's equation in characteristic three
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 149-150
-
- Article
-
- You have access
- Export citation
Infinitary harmonic numbers
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 151-158
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian Ph.D. theses
Distributions on bicoloured evolutionary trees
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 159-160
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 41 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
BAZ volume 41 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

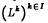 of self-adjoint linear operators of Hilbert-Schmidt class on
of self-adjoint linear operators of Hilbert-Schmidt class on 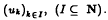 . It is shown that with the norm | ‖
. It is shown that with the norm | ‖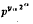 , where
, where 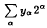 (where
(where