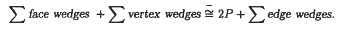This note presents an analogue of the classical Heisenberg-Weyl uncertainty principle for the Dunkl transform on ℝN. Its proof is based on expansions with respect to generalised Hermite functions.

Roughly speaking, we show that a Banach space X has the fixed point property for nonexpansive mappings whenever X has the WORTH property and the unit sphere of X does not contain a triangle with sides of length larger than 2.

A characterisation is given of all (finitely additive) spectral measures in a Banach space (and defined on an algebra of sets) which satisfy a Lipschitz condition. This also corrects (slightly) an analogous result in the more specialised setting of resolutions of the identity of scalar-type spectral operators (due to C.A. McCarthy).

The recently introduced two-parameter eight-state Uq [gl(3|1)] supersymmetric fermion model is extended to include boundary terms. Nine classes of boundary conditions are constructed, all of which are shown to be integrable via the graded boundary quantum inverse scattering method. The boundary systems are solved by using the coordinate Bethe ansatz and the Bethe ansatz equations are given for all nine cases.

Polytopes of roots of type An−1 are investigated, which we call Pn. The polytopes, , of positive roots and the origin have been considered in relation to other branches of mathematics [4]. We show that exactly n copies of forms a disjoint cover of Pn. Moreover, those n copies of can be obtained by letting the elements of a subgroup of the symmetric group Sn generated by an n-cycle act on . We also characterise the faces of Pn and some facets of , which we believe to be useful in some optimisation problems. As by-products, we obtain an interesting identity on the number of lattice paths and a triangulation of the product of two simplices.

We study images of Hankel operators on the Bergman or Hardy space of the poly-disk. We give characterisations of pairs of antiholomorphic symbols inducing Hankel operators whose images are mutually orthogonal.

Every group acts transitively by conjugation on each of its conjugacy classes of elements. It is natural to wonder when this action becomes multiply transitive. In this paper, we determine all finite groups which act faithfully and 2-transitively on a conjugacy class of elements. We also give some consequences including a solvability criterion based on what fraction of elements belong to conjugacy classes upon which the group acts faithfully and 2–transitively.

Let G be a Hausdorff topological group and μ and λ be probability measures on G. We prove necessary and sufficient conditions for the existence of a probability measure ρ such that λ * ρ * μ = ρ under certain conditions. We prove a similar result for probability measures on semigroups.

Andersson obtained weighted Lp estimates for on analytic polyhedra. We provide an example to show why they cannot be improved.

In this paper, we first prove a fixed point theorem for a family of multivalued maps defined on product spaces. We then apply our result to prove an equilibrium existence theorem for an abstract economy. We also consider a system of variational inequalities and prove the existence of its solutions by using our fixed point theorem.

In this note we extend a result of Drewnowski concerning copies of C0 in the Banach space of all countably additive vector measures and study some properties of complemented copies of C0 in several Banach spaces of vector measures.

We study weak convergence of tensor products of vector measures with values in nuclear spaces, such as the space of all rapidly decreasing, infinitely differentiable functions, the space of all test functions, and the strong duals of those spaces. It is shown that the weak convergence of a net of tensor products of vector measures follows from that of the corresponding net of real product measures.

According to results of Heineken and Stadelmann, a non-torsion group is a 2-Baer group if and only if it is 2-Engel, and it has all subgroups 2-subnormal if and only if it is nilpotent of class 2. We extend some of these results to values of n greater than 2. Any non-torsion group which is an n-Baer group is an n-Engel group. The converse holds for n = 3, and for all n in the case of metabelian groups. A non-torsion group without involutions having all subgroups 3-subnormal has nilpotency class 4, and this bound is sharp.

Let D be an integral domain with quotient field K. If α2 − α ∈ D and α3 − α2 ∈ D imply α ∈ D for all elements α of K, then D is called a u-closed domain. A submonoid S of a torsion-free Abelian group is called a grading monoid. We consider the semigroup ring D[S] of a grading monoid S over a domain D. The main aim of this note is to determine conditions for D[S] to be u-closed. We shall show the following Theorem: D[S] is u-closed if and only if D is u-closed.

It is well known that Q is a simple quasigroup if and only if Mlt Q acts primitively on Q. Here we show that Q is a simple quasigroup if and only if Mlt Q acts quasiprimitively on Q, and that Q is a simple right quasigroup if and only if RMlt Q acts quasiprimitively on Q.

Let n be a positive integer, and let (a, b, c) be a primitive Pythagorean triple. In this paper we give certain conditions for the equation (an)x + (bn)y = (cn)z to have positive integer solutions (x, y, z) with (x, y, z) ≠ (2, 2, 2). In particular, we show that x, y and z must be distinct.

In this paper we establish a generalised KKM theorem from which many well-known KKM theorems and a fixed point theorem of Tarafdar are extended.

In this paper we present an elementary proof of a congruence by subtraction relation. In order to prove congruence by subtraction, we produce a dissection relating equal sub-polytopes. An immediate consequence of this relation is an Euler-type volume identity in ℝ3 which appeared in the Unsolved Problems section of the December 1996 MAA Monthly.

This Euler-type volume identity relates the volumes of subsets of a polytope called wedges that correspond to its faces, edges, and vertices. A wedge consists of the inward normal chords of the polytope emanating from a face, vertex, or edge. This identity is stated in the theorem below.

Euler Volume Theorem. For any three dimensional convex polytope P

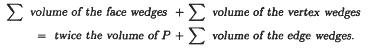
This identity follows immediately from

We derive the formula in the title and deduce some consequences. For example we show that the identity map from any compact manifold to itself is always stable as an exponentially harmonic map. This is in sharp contrast to the harmonic or p-harmonic cases where many such identity maps are unstable. We also prove that an isometric and totally geodesic immersion of Sm into Sn is an unstable exponentially harmonic map if m ≠ n and is a stable exponentially harmonic map if m = n.

If a Banach space X contains a complemented subspace isomorphic to ℓ1 and if ε > 0, then there exists a subspace Y of X and a projection P from X onto Y such that Y is (1 + ε)-isometric to ℓ1 and ∥P∥ ≤ 1 + ε. A stronger result for c0 is proved for Banach spaces whose dual unit ball is weak sequentially compact.