Editorial
Editorial
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 1-2
-
- Article
-
- You have access
- Export citation
Research Article
On a relation between the Fitting length of a soluble group and the number of conjugacy classes of its maximal nilpotent subgroups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 3-10
-
- Article
-
- You have access
- Export citation
Free products and residual nilpotency
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 11-13
-
- Article
-
- You have access
- Export citation
Metabelian groups and varieties
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 15-25
-
- Article
-
- You have access
- Export citation
Schunk classes are nilpotent product closed
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 27-28
-
- Article
-
- You have access
- Export citation
Surface and internal waves in a liquid of variable depth
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 29-46
-
- Article
-
- You have access
- Export citation
Adjunction semigroups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 47-58
-
- Article
-
- You have access
- Export citation
On a new finite non–abelian simple group of Janko
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 59-79
-
- Article
-
- You have access
- Export citation
Optimal quadrature
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 81-108
-
- Article
-
- You have access
- Export citation
An extension of the Krull-Schmidt theorem
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 109-114
-
- Article
-
- You have access
- Export citation
Representing N-semigroups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 115-125
-
- Article
-
- You have access
- Export citation
Surface and internal waves in a liquid of variable depth
-
- Published online by Cambridge University Press:
- 01 August 1969, pp. 29-46
-
- Article
-
- You have access
- Export citation
Semifield metric spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 127-136
-
- Article
-
- You have access
- Export citation
A theorem on homeomorphism groups and products of spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 137-141
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian Ph.D. theses
The deficiency of finite groups
-
- Published online by Cambridge University Press:
- 17 April 2009, p. 143
-
- Article
-
- You have access
- Export citation
Equations of heat conduction with slow combustion
-
- Published online by Cambridge University Press:
- 17 April 2009, p. 144
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 1 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
BAZ volume 1 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 1 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 01 August 1969, pp. f1-f2
-
- Article
-
- You have access
- Export citation

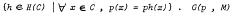 is a group.
is a group.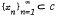 and a sequence
and a sequence 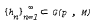 such that
such that