A survey is made of the way in which a variety of physical scalar and vector quantities are diffused, and convected out of fixed regions in moving fluids. In particular, viscous flow itself is viewed as the diffusion and convection of circulation which is generated at the boundaries of the fluid by the no-slip condition. The non-linearity of the problem arises from the fact that the convection field is in part self-generated by the diffused circulation. Ways of overcoming these difficulties are reviewed in the light of the above point of view. New kinematic interpretations are given for the equations governing axisymmetric viscous flow and these are used to determine the flow vector for ring circulation, angular momentum and other relevant physical quantities.

This paper continues the invèstigation of varieties of topological groups. It is shown that the family of all varieties of topological groups with any given underlying algebraic variety is a class and not a set. In fact the family of all β-varieties with any given underlying algebraic variety is a class and not a set. A variety generated by a family of topological groups of bounded cardinal is not a full variety.

The varieties V(R) and V(T) generated by the additive group of reals and the circle group respectively each with its usual topology are examined. In particular it is shown that a locally compact Hausdorff abelian group is in V(T) if and only if it is compact. Thus V(R) properly contains V(T).

It is proved that any free topological group of a non-indiscrete variety is disconnected. Finally, some comments are made on topologies on free groups.

An order on the collection of totally unordered subsets of a partially well ordered set is defined, shown to satisfy the descending chain condition but not to be necessarily a partial well order itself.

The Main Theorems of P. Turán's book Eine neue Methode in der Analysis und deren Anwendungen concern only sums of powers but are easily generalised to exponential sums with polynomial coefficients. It does not appear to have been observed however, that similar such theorems with analogous implication as to value distribution and arithmetical behaviour can be formulated for a wider class of functions. 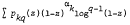We prove a result for functions of the form subsuming identities which Mahler has shown to contain transcendence results on the exponential and logarithmic functions and diophantine results of the Thue-Siegel-Roth type.

An integral manifold for a system of differential equations is a manifold such that any solution of the equations which has a point on it is entirely contained on it. The method of averaging establishes the existence of such a manifold for a system which is a perturbation of an autonomous system with a periodic orbit. The existence of the manifold is established here under more general hypotheses, namely for perturbations which are ‘integrally small’. The method differs from the original method of Bogolyubov and Mitropolskii and operates directly with the individual solutions. This is made possibly by the use of an appropriate norm, and is equivalent to solving the partial differential equation which occurs in work by Moser and Sacker by the method of characteristics rather than by the introduction of an artificial viscosity term. Moreover, detailed smoothness properties of the manifold are obtained. For periodic perturbations the integral manifold is a torus and these smoothness properties are just sufficient to permit the application of Denjoy's theorem.

Under weak hypotheses, the geometric ergodicity of the states of a subcritical branching process with immigration is demonstrated by obtaining an asymptotic representation of the transition probabilities.

We give an elementary and self-contained proof of the result that the sheaf M~ determined by an injective module M over a commutative noetherian ring is flasque.

It is shown in this note that if Q is an algebra of uniformly bounded mean-square continuous real-valued random functions indexed in a compact set T, containing all bounded random variables and separating points of T (i.e., given t1 and t2 in T, there is a random function Xt in Q such that , then given any mean square continuous random function, there is a sequence in Q converging in mean square to the given random function uniformly on T.

A new method is found for solving the general Dirichlet problem for two non-overlapping spheres of different radius. The expression for the external potential involves hypergeometric functions and is obtained from an infinite set of linear equations. In essence the method makes use of the fact that (I–A)–1 = I + A + A2 + A3 + …, where A belongs to a certain class of infinite matrices and I is the unit matrix.

An analogue of the theorem on the existence of a primitive element for separable extensions of fields is presented for semigroups. This has two immediate consequences.

(i) A semigroup is algebraically closed with respect to equations in several variables if and only if it is closed with respect to equations in a single variable.

(ii) Any countable semigroup C is embedded in a two-generator semigroup, one of whose generators is in C.

Further, a proof is given that any free product of a semigroup of order one with one of order two is SQ–universal, that is, its factor semigroups embed all countable semigroups. The proofs are adaptations of one used by Trevor Evans, Proc. Amer. Math. Soc. 3 (1952), 614–620. to show that a free product of two infinite cyclic semigroups is SQ–universal.

Let A1, A2 be Banach algebras, A1 ⊗ A2 their algebraic tensor product over the complex field. If ‖ · ‖α is an algebra norm on A1 ⊗ A2 we write A1 ⊗αA2 for the ‖ · ‖α-completion of A1 ⊗ A2. In this note we study the existence of identities and approximate identities in A1 ⊗αA2 versus their existence in A1 and A2. Some of the results obtained are already known, but our method of proof appears new, though it is quite elementary.

Gillman-Henriksen have defined a class of spaces, containing the discrete spaces and their Stone-Čech compactifications, called F'-spaces. The dyadic spaces are the continuous images of products of finite discrete spaces – a class which contains the compact metric spaces and all compact topological groups. In this paper it is shown that F'-spaces have no infinite dyadic sutspaces and, almost always, no dyadic compactifications. An interesting corollary is that if βX \ X is dyadic, then X is pseudocompact.

If G is a finite group and P is a group-theoretic property, G will be called P-max-core if for every maximal subgroup M of G, M/MG has property P where MG = ∩ is the core of M in G. In a joint paper with John D. Dixon and A.H. Rhemtulla, we showed that if p is an odd prime and G is (p-nilpotent)-max-core, then G is p-solvable, and then using the techniques of the theory of solvable groups, we characterized nilpotent-max-core groups as finite nilpotent-by-nilpotent groups. The proof of the first result used John G. Thompson's p-nilpotency criterion and hence required p > 2. In this paper I show that supersolvable-max-core groups (and hence (2-nilpotent)-max-core groups) need not be 2-solvable (that is, solvable). Also I generalize the second result, among others, and characterize (p-nilpotent)-max-core groups (for p an odd prime) as finite nilpotent-by-(p-nilpotent) groups.

A characterization is obtained of the types τ for which [G/G(τ)](τ) = 0 for all torsion-free abelian groups G.