Research Article
Congruences on distributive pseudocomplemented lattices
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 161-179
-
- Article
-
- You have access
- Export citation
A generalization of a theorem of Wedderburn
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 181-185
-
- Article
-
- You have access
- Export citation
The classification of some spherically symmetric space-time metrics
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 187-190
-
- Article
-
- You have access
- Export citation
Arithmetical properties of the digits of the multiples of an irrational number
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 191-203
-
- Article
-
- You have access
- Export citation
A characterization of weak projectability
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 205-209
-
- Article
-
- You have access
- Export citation
A constructive proof of Gelbaum's theorem on tensor products
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 211-214
-
- Article
-
- You have access
- Export citation
A Fritz John theorem in complex space
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 215-220
-
- Article
-
- You have access
- Export citation
Axioms for constructive fields
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 221-232
-
- Article
-
- You have access
- Export citation
Torsion theories and coherent rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 233-239
-
- Article
-
- You have access
- Export citation
Rudin-Shapiro sequences on compact groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 241-245
-
- Article
-
- You have access
- Export citation
On a class of diophantine inequalities
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 247-259
-
- Article
-
- You have access
- Export citation
The Jacobi-Perron algorithm and the algebra of recursive sequences
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 261-277
-
- Article
-
- You have access
- Export citation
Spectral approximation theorems for bounded linear operators
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 279-287
-
- Article
-
- You have access
- Export citation
Divergence of Fourier series
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 289-304
-
- Article
-
- You have access
- Export citation
On soluble groups which admit the dihedral group of order eight fixed-point-freely
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 305-312
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian PhD theses
Green's relations in semigroups of functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 313-314
-
- Article
-
- You have access
- Export citation
Ultraproducts and higher order models
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 315-316
-
- Article
-
- You have access
- Export citation
Corrigenda
Corrigendum: On the relation of a distributive lattice to its lattice of ideals
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 317-318
-
- Article
-
- You have access
- Export citation
Corrigendum: Block idempotents and the Brauer correspondence
-
- Published online by Cambridge University Press:
- 17 April 2009, p. 319
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 8 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation

 ,
, 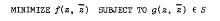
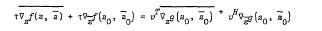
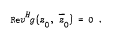
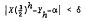
 is only congruent modulo rad
is only congruent modulo rad . The theorem still holds if θ(rad
. The theorem still holds if θ(rad