Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-27T21:05:25.406Z Has data issue: false hasContentIssue false
  • English
  • Français

Weak and semi-strong solutions of the Schneider-Tricomi problem in the euclidean plane

Published online by Cambridge University Press:  17 April 2009

John M.S. Rassias
John M.S. Rassias
Affiliation:
National Metsovion Polytechnic School, Chair of Mathematics A′, Athens, Greece.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Schneider (Math. Nachr. 60 (1974), 167–180) has established the following result. Consider the mixed type equation

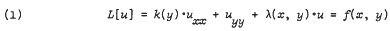
in G ⊂ R2 which is a simply connected region, bounded for y > 0 by a piece-wise smooth curve Γ0 connecting the points A(0, 0) and B(1, 0), and for y < 0 by the solutions of k(y).(dy)2 + (dx)2 = 0 which meet at the point G(½, yc), such that 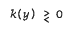for ,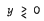

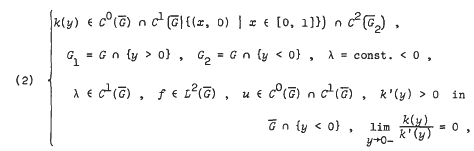
S(x, y) = F(yy) + 8λ·(k/k′)2 > 0 in Ḡ ∩ {y < 0}, “Schneider's Condition”, where F(y) = 1 + 2(k/k′)′, and such that S = S(x, y) is integrable in G2, 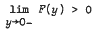“Frankl's Condition”. Then the Tricomi Problem (T): L[u] = f with 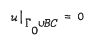has a weak solution u ∈ L2(Ḡ) and the Adjoint Tricomi Problem (T+): L+[w] = f with 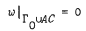has at most one semistrong solution.

In this present paper we get the above result of Schneider in a much more generalized way, so that here our uniqueness theorem and existence results include cases where S(x, y) may be negative in G2.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 20 , Issue 2 , April 1979 , pp. 187 - 192
Copyright
Copyright © Australian Mathematical Society 1979

References

[1]Berezanskiiˇ, Ju.M., Expansions in eigenfunctions of selfadjoint operators (Translations of Mathematical Monographs, 17. American Mathematical Society, Providence, Rhode Island, 1968).Google Scholar
[2]Франль, Ф.И. [Frankl, F.], “О задачах C.A. Чаплыгина для смешанных до- и сверхзвуновых течений” [On the problems of Chaplygin for mixed sub- and supersonic flows], Bull. Acad. Sci. URSS Sér. Math. [Izv. Akad. Nauk SSSR] 9 (1945), 121–143.Google Scholar
[3]Protter, M.H., “Uniqueness theorems for the Tricomi problem”, J. Rational Meoh. Anal. 2 (1953), 107–114.Google Scholar
[4]Rassias, John Michael, “Mixed type partial differential equations in Rn” (PhD dissertation, University of California, Berkeley, 1977).Google Scholar
[5]Schneider, Manfred, “Über schwache und halbstarke Lösungen des Tricomi-Problems”, Math. Nachr. 60 (1974), 167–180.Google Scholar