Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-02-04T15:11:06.309Z Has data issue: false hasContentIssue false
  • English
  • Français

Universality of methods approximating the derivative

Published online by Cambridge University Press:  17 April 2009

Gerd Herzog  and
Roland Lemmert
Gerd Herzog
Affiliation:
Mathematisches Institut I, Universität Karlsruhe, D-76128 Karlsruhe, Germany, e-mail: [email protected]: [email protected]
Roland Lemmert
Affiliation:
Mathematisches Institut I, Universität Karlsruhe, D-76128 Karlsruhe, Germany, e-mail: [email protected]: [email protected]
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove the existence of universal functions for mappings Tn: C([0,1]) → Lp([0,1]), 0 < p < 1, with Tn(f) → f′ (n → ∞) on certain subsets of C1([0,1]). As an application we conclude that there are continuous functions f ∈ C([0,1]), such that the derivatives of the Bernstein polynomials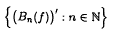 form a dense subset of Lp([0,1]) for each 0 < p < 1.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 73 , Issue 3 , June 2006 , pp. 405 - 411
Copyright
Copyright © Australian Mathematical Society 2006

References

[1]Bogmér, A. and Sövegjártó, A., ‘On universal functions’, Acta Math. Hungar. 49 (1987), 237–239.CrossRefGoogle Scholar
[2]Buczolich, Z., ‘On universal functions and series’, Acta Math. Hungar. 49 (1987), 403–414.CrossRefGoogle Scholar
[3]Day, M.M., ‘The spaces L P with 0 < p < 1’, Bull. Amer. math. Soc. 46 (1940), 816–823.CrossRefGoogle Scholar
[4]Grosse-Erdmann, K.-G., ‘Universal families and hypercyclic operators’, Bull. Amer. Math. Soc. (N.S.) 36 (1999), 345–381.CrossRefGoogle Scholar
[5]Herzog, G., ‘On universal functions and interpolation’, Analysis 11 (1991), 21–26.CrossRefGoogle Scholar
[6]Joó, I., ‘On the divergence of eigenfunction expansions’, Ann. Univ. Sci. Budapest Eötvös Sect. Math. 32 (1989), 3–36.Google Scholar
[7]Lorentz, G.G., Bernstein polynomials, Mathematical Expositions 8 (University of Toronto Press X, Toronto, 1953).Google Scholar
[8]Marcinkiewicz, J., ‘Sur les nombres dérivés.’, Fund. Math. 24 (1935), 305–308.CrossRefGoogle Scholar