Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-30T19:30:20.022Z Has data issue: false hasContentIssue false
  • English
  • Français

UNIQUE REPRESENTATION BI-BASIS FOR THE INTEGERS

Part of: Sequences and sets

Published online by Cambridge University Press:  12 September 2013

RAN XIONG  and
MIN TANG
RAN XIONG
Affiliation:
School of Mathematics and Computer Science, Anhui Normal University, Wuhu 241003, China email [email protected]
MIN TANG*
Affiliation:
School of Mathematics and Computer Science, Anhui Normal University, Wuhu 241003, China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For 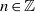$n\in \mathbb{Z} $ and 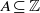$A\subseteq \mathbb{Z} $, let 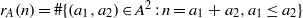${r}_{A} (n)= \# \{ ({a}_{1} , {a}_{2} )\in {A}^{2} : n= {a}_{1} + {a}_{2} , {a}_{1} \leq {a}_{2} \} $ and 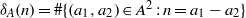${\delta }_{A} (n)= \# \{ ({a}_{1} , {a}_{2} )\in {A}^{2} : n= {a}_{1} - {a}_{2} \} $. We call 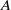$A$ a unique representation bi-basis if 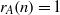${r}_{A} (n)= 1$ for all 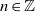$n\in \mathbb{Z} $ and 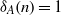${\delta }_{A} (n)= 1$ for all 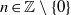$n\in \mathbb{Z} \setminus \{ 0\} $. In this paper, we construct a unique representation bi-basis of $ \mathbb{Z} $ whose growth is logarithmic.

Keywords

bi-basisrepresentation function

MSC classification

Secondary: 11B34: Representation functions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 89 , Issue 3 , June 2014 , pp. 460 - 465
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Chen, Y. G., ‘The difference basis and bi-basis of ${ \mathbb{Z} }_{m} $’, J. Number Theory 130 (2010), 716–726.CrossRefGoogle Scholar
Cilleruelo, J. and Nathanson, M. B., ‘Perfect difference sets constructed from Sidon sets’, Combinatorica 28 (2008), 401–414.CrossRefGoogle Scholar
Lee, J., ‘Infinitely often dense bases for the integers with a prescribed representation function’, Integers 10 (2010), 299–307.CrossRefGoogle Scholar
Nathanson, M. B., ‘Unique representation bases for integers’, Acta Arith. 108 (2003), 1–8.CrossRefGoogle Scholar
Tang, M., ‘Dense sets of integers with a prescribed representation function’, Bull. Aust. Math. Soc. 84 (2011), 40–43.CrossRefGoogle Scholar
Tang, C. W., Tang, M. and Wu, L., ‘Unique difference bases of $ \mathbb{Z} $’, J. Integer Seq. 14 (2011), Article 11.1.8.Google Scholar