Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T04:05:56.188Z Has data issue: false hasContentIssue false
  • English
  • Français

TWO NEW LOWER BOUNDS FOR THE SPARK OF A MATRIX

Part of: Combinatorics

Published online by Cambridge University Press:  08 June 2017

HAIFENG LIU Open the ORCID record for HAIFENG LIU [Opens in a new window] ,
JIHUA ZHU  and
JIGEN PENG
HAIFENG LIU*
Affiliation:
School of Mathematics and Statistics, Xi’an Jiaotong University, Xi’an 710049, China email [email protected]
JIHUA ZHU
Affiliation:
School of Software Engineering, Xi’an Jiaotong University, Xi’an 710049, China email [email protected]
JIGEN PENG
Affiliation:
School of Mathematics and Statistics, Xi’an Jiaotong University, Xi’an 710049, China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The 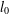$l_{0}$-minimisation problem has attracted much attention in recent years with the development of compressive sensing. The spark of a matrix is an important measure that can determine whether a given sparse vector is the solution of an 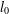$l_{0}$-minimisation problem. However, its calculation involves a combinatorial search over all possible subsets of columns of the matrix, which is an NP-hard problem. We use Weyl’s theorem to give two new lower bounds for the spark of a matrix. One is based on the mutual coherence and the other on the coherence function. Numerical examples are given to show that the new bounds can be significantly better than existing ones.

Keywords

lower boundsparkmutual coherencecoherence functioncompressive sensing

MSC classification

Primary: 05A20: Combinatorial inequalities
Secondary: 90C27: Combinatorial optimization
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 96 , Issue 3 , December 2017 , pp. 353 - 360
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

Footnotes

H. F. Liu, J. H. Zhu and J. G. Peng are supported by the Natural Science Foundation of China (Grant Nos. 11401463, 61573273 and 11131006) and the Fundamental Research Funds for the Central Universities.

References

Candes, E. J. and Tao, T., ‘Near-optimal signal recovery from random projections: universal encoding strategies?’, IEEE Trans. Inform. Theory 52 (2006), 5406–5425.CrossRefGoogle Scholar
Donoho, D. L., ‘Compressed sensing’, IEEE Trans. Inform. Theory 52 (2006), 1289–1306.CrossRefGoogle Scholar
Donoho, D. L. and Elad, M., ‘Optimally sparse representation in general (nonorthogonal) dictionaries via l 1 minimization’, Proc. Natl. Acad. Sci. USA 100 (2003), 2197–2202.Google Scholar
Donoho, D. L. and Huo, X. M., ‘Uncertainty principles and ideal atomic decomposition’, IEEE Trans. Inform. Theory 47 (2001), 2845–2862.Google Scholar
Elad, M., Sparse and Redundant Representations (Springer, New York, 2010).CrossRefGoogle Scholar
Foucart, S. and Rauhut, H., A Mathematical Introduction to Compressive Sensing (Springer, New York, 2013).Google Scholar
Giryes, R., Nam, S., Elad, M., Gribonval, R. and Davies, M. E., ‘Greedy-like algorithms for cosparse analysis model’, Linear Algebra Appl. 441 (2014), 22–60.Google Scholar
Horn, R. A. and Johnson, C. R., Matrix Analysis, 2nd edn (Cambridge University Press, Cambridge, 2013).Google Scholar
Rauhut, H. and Schwab, C., ‘Compressive sensing Petrov–Galerkin approximation of high-dimensional parametric operator equations’, Math. Comp. 86 (2017), 661–700.CrossRefGoogle Scholar
Tillmann, A. M. and Pfetsch, M. E., ‘The computational complexity of the restricted isometry property, the nullspace property and related concepts in compressive sensing’, IEEE Trans. Inform. Theory 60 (2014), 1248–1259.Google Scholar
Tropp, J. A., ‘Greed is good: algorithm results for sparse approximation’, IEEE Trans. Inform. Theory 50 (2004), 2231–2242.Google Scholar
Xiao, Y. H. and Zhu, H., ‘A conjugate gradient method to solve convex constrained monotone equations with applications in compressive sensing’, J. Math. Anal. Appl. 405 (2013), 310–319.CrossRefGoogle Scholar