Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-19T03:11:45.291Z Has data issue: false hasContentIssue false
  • English
  • Français

TRIVIALITY OF THE GENERALISED LAU PRODUCT ASSOCIATED TO A BANACH ALGEBRA HOMOMORPHISM

Part of: Topological algebras, normed rings and algebras, Banach algebras

Published online by Cambridge University Press:  01 March 2016

YEMON CHOI
YEMON CHOI*
Affiliation:
Department of Mathematics and Statistics, Lancaster University, Lancaster, LA1 4YF, UK email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

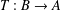Several papers have, as their raison d’être, the exploration of the generalised Lau product associated to a homomorphism $T:B\rightarrow A$ of Banach algebras. In this short note, we demonstrate that the generalised Lau product is isomorphic as a Banach algebra to the usual direct product 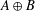$A\oplus B$. We also correct some misleading claims made about the relationship between this generalised Lau product and an older construction of Monfared [‘On certain products of Banach algebras with applications to harmonic analysis’, Studia Math. 178(3) (2007), 277–294].

Keywords

generalised Lau product

MSC classification

Primary: 46H20: Structure, classification of topological algebras
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 94 , Issue 2 , October 2016 , pp. 286 - 289
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Abtahi, F. and Ghafarpanah, A., ‘A note on cyclic amenability of the Lau product of Banach algebras defined by a Banach algebra morphism’, Bull. Aust. Math. Soc. 92(2) (2015), 282–289.CrossRefGoogle Scholar
Abtahi, F., Ghafarpanah, A. and Rejali, A., ‘Biprojectivity and biflatness of Lau product of Banach algebras defined by a Banach algebra morphism’, Bull. Aust. Math. Soc. 91(1) (2015), 134–144.CrossRefGoogle Scholar
Bhatt, S. J. and Dabhi, P. A., ‘Arens regularity and amenability of Lau product of Banach algebras defined by a Banach algebra morphism’, Bull. Aust. Math. Soc. 87(2) (2013), 195–206.CrossRefGoogle Scholar
Dabhi, P. A., Jabbari, A. and Haghnejad Azar, K., ‘Some notes on amenability and weak amenability of Lau product of Banach algebras defined by a Banach algebra morphism’, Acta Math. Sin. (Engl. Ser.) 31(9) (2015), 1461–1474.CrossRefGoogle Scholar
Javanshiri, H. and Nemati, M., ‘On a certain product of Banach algebras and some of its properties’, Proc. Rom. Acad. Ser. A Math. Phys. Tech. Sci. Inf. Sci. 15(3) (2014), 219–227.Google Scholar
Javanshiri, H. and Nemati, M., ‘The multiplier algebra and BSE-functions for certain product of Banach algebras’, Preprint, 2015, arXiv:1509.00895.Google Scholar
Khoddami, A. R., ‘ n-weak amenability of T-Lau product of Banach algebras’, Chamchuri J. Math. 5 (2013), 57–65.Google Scholar
Khoddami, A. R., ‘On Banach algebras induced by a certain product’, Chamchuri J. Math. 6 (2014), 89–96.Google Scholar
Monfared, M. S., ‘On certain products of Banach algebras with applications to harmonic analysis’, Studia Math. 178(3) (2007), 277–294.CrossRefGoogle Scholar
Nemati, M. and Javanshiri, H., ‘Some homological and cohomological notions on T-Lau product of Banach algebras’, Banach J. Math. Anal. 9(2) (2015), 183–195.Google Scholar
Pourabbas, A. and Razi, N., ‘Some homological properties of $T$ -Lau product algebra’. Preprint, 2014, arXiv:1411.0112.Google Scholar
Pourabbas, A. and Razi, N., ‘Cohomological characterization of $T$ -Lau product algebras’. Preprint, 2015, arXiv:1509.01933.Google Scholar