No CrossRef data available.
Article contents
TRANSVERSALS AS GENERATING SETS IN FINITELY GENERATED GROUPS
Part of:
Special aspects of infinite or finite groups
Structure and classification of infinite or finite groups
Published online by Cambridge University Press: 19 August 2015
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
We explore transversals of finite index subgroups of finitely generated groups. We show that when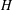 
$H$ is a subgroup of a rank-
$n$ group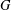 
$G$ and 
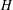$H$ has index at least 
$n$ in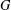 
$G$, we can construct a left transversal for 
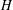$H$ which contains a generating set of size 
$n$ for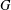 
$G$; this construction is algorithmic when 
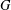$G$ is finitely presented. We also show that, in the case where 
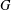$G$ has rank 
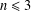$n\leq 3$, there is a simultaneous left–right transversal for 
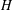$H$ which contains a generating set of size 
$n$ for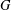 
$G$. We finish by showing that if 
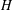$H$ is a subgroup of a rank-
$n$ group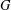 
$G$ with index less than 
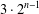$3\cdot 2^{n-1}$, and 
$H$ contains no primitive elements of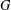 
$G$, then 
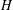$H$ is normal in 
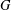$G$ and 
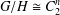$G/H\cong C_{2}^{n}$.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © 2015 Australian Mathematical Publishing Association Inc.
References
Blass, A., ‘Injectivity, projectivity, and the axiom of choice’, Trans. Amer. Math. Soc. 255 (1979), 31–59.CrossRefGoogle Scholar
Button, J., Chiodo, M. and Laris, M. Zeron-Medina, ‘Coset intersection graphs, and transversals as generating sets for finitely generated groups’, in: Extended Abstracts Fall 2012, Trends in Mathematics: Automorphisms of Free Groups, 1 (eds. González-Meneses, J. et al. ) (Springer, New York, 2014), 29–34.CrossRefGoogle Scholar
Button, J., Chiodo, M. and Laris, M. Zeron-Medina, ‘Coset intersection graphs for groups’, Amer. Math. Monthly 121(10) (2014), 922–926.CrossRefGoogle Scholar
Cameron, P., ‘Generating a group by a transversal’, Preprint available athttp://www.maths.qmul.ac.uk/ pjc/preprints/transgenic.pdf.Google Scholar
Cameron, P., ‘Problem 100 from a problem set’, available athttp://www.maths.qmul.ac.uk/∼pjc/oldprob.html.Google Scholar
Clifford, A. and Goldstein, R., ‘Subgroups of free groups and primitive elements’, J. Group Theory 13 (2010), 601–611.CrossRefGoogle Scholar
Evans, M. J., ‘Primitive elements in free groups’, Proc. Amer. Math. Soc. 106 (1989), 313–316.CrossRefGoogle Scholar
Lubotzky, A. and Segal, D., Subgroup Growth, Progress in Mathematics, 212 (Birkhaüser, Basel, 2003).CrossRefGoogle Scholar
Pak, I., ‘What do we know about the product replacement algorithm?’, in: Groups and Computation, III, Ohio State Univ. Math. Res. Inst. Publ. 8 (de Gruyter, Berlin, 2001), 301–347.CrossRefGoogle Scholar
Parzanchevski, O. and Puder, D., ‘Measure preserving words are primitive’, J. Amer. Math. Soc. 28 (2015), 63–97.Google Scholar
Roig, A., Ventura, E. and Weil, P., ‘On the complexity of the Whitehead minimization problem’, Internat. J. Algebra Comput. 17(8) (2007), 1611–1634.CrossRefGoogle Scholar
Whiston, J., ‘Maximal independent generating sets of the symmetric group’, J. Algebra 232 (2000), 255–268.CrossRefGoogle Scholar
Whitehead, J. H. C., ‘On equivalent sets of elements in a free group’, Ann. of Math. (2) 37(4) (1936), 782–800.CrossRefGoogle Scholar
You have
Access