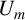1. Mahler’s and Koksma’s classifications of p-adic numbers
Let p be a prime number and let
![]() $|\cdot |_{p}$
denote the p-adic absolute value on the field
$|\cdot |_{p}$
denote the p-adic absolute value on the field
![]() $\mathbb {Q}$
of rational numbers, normalised such that
$\mathbb {Q}$
of rational numbers, normalised such that
![]() $|p|_{p}=p^{-1}$
. The completion of
$|p|_{p}=p^{-1}$
. The completion of
![]() $\mathbb {Q}$
with respect to
$\mathbb {Q}$
with respect to
![]() $|\cdot |_{p}$
is the field
$|\cdot |_{p}$
is the field
![]() $\mathbb {Q}_{p}$
of p-adic numbers, and the unique extension of
$\mathbb {Q}_{p}$
of p-adic numbers, and the unique extension of
![]() $|\cdot |_{p}$
to the field
$|\cdot |_{p}$
to the field
![]() $\mathbb {Q}_{p}$
is denoted by the same notation
$\mathbb {Q}_{p}$
is denoted by the same notation
![]() $|\cdot |_{p}$
. Mahler [Reference Mahler16] gave a classification of p-adic numbers in analogy with his classification [Reference Mahler15] of real numbers, as follows. Let
$|\cdot |_{p}$
. Mahler [Reference Mahler16] gave a classification of p-adic numbers in analogy with his classification [Reference Mahler15] of real numbers, as follows. Let
![]() $P(x)=a_{n}x^{n}+\cdots +a_{1}x+a_{0}$
be a nonzero polynomial in x over the ring
$P(x)=a_{n}x^{n}+\cdots +a_{1}x+a_{0}$
be a nonzero polynomial in x over the ring
![]() $\mathbb {Z}$
of rational integers. We denote by
$\mathbb {Z}$
of rational integers. We denote by
![]() $\deg (P)$
the degree of
$\deg (P)$
the degree of
![]() $P(x)$
with respect to x. The height
$P(x)$
with respect to x. The height
![]() $H(P)$
of
$H(P)$
of
![]() $P(x)$
is defined by
$P(x)$
is defined by
![]() $H(P)=\max \{|a_{n}|,\ldots ,|a_{1}|, |a_{0}|\}$
, where
$H(P)=\max \{|a_{n}|,\ldots ,|a_{1}|, |a_{0}|\}$
, where
![]() $|\cdot |$
denotes the usual absolute value on the field
$|\cdot |$
denotes the usual absolute value on the field
![]() $\mathbb {R}$
of real numbers. Let
$\mathbb {R}$
of real numbers. Let
![]() $\xi $
be any p-adic number and let n, H be any positive rational integers. Following Bugeaud [Reference Bugeaud3], set
$\xi $
be any p-adic number and let n, H be any positive rational integers. Following Bugeaud [Reference Bugeaud3], set
 $$ \begin{align*} w_{n}(\xi)=\limsup_{H \rightarrow \infty}\frac{-\log (H w_{n}(H, \xi))}{\log H} \quad\textrm{and}\quad w(\xi)=\limsup_{n \rightarrow \infty}\frac{w_{n}(\xi)}{n}. \end{align*} $$
$$ \begin{align*} w_{n}(\xi)=\limsup_{H \rightarrow \infty}\frac{-\log (H w_{n}(H, \xi))}{\log H} \quad\textrm{and}\quad w(\xi)=\limsup_{n \rightarrow \infty}\frac{w_{n}(\xi)}{n}. \end{align*} $$
Then
![]() $\xi $
is called:
$\xi $
is called:
-
• a p-adic A-number if
 $w(\xi )=0$
;
$w(\xi )=0$
; -
• a p-adic S-number if
 $0< w(\xi )<\infty $
;
$0< w(\xi )<\infty $
; -
• a p-adic T-number if
 $w(\xi )=\infty $
and
$w(\xi )=\infty $
and
 $w_{n}(\xi )<\infty $
for
$w_{n}(\xi )<\infty $
for
 $n=1,2,3,\ldots $
; and
$n=1,2,3,\ldots $
; and -
• a p-adic U-number if
 $w(\xi )=\infty $
and
$w(\xi )=\infty $
and
 $w_{n}(\xi )=\infty $
from some n onward.
$w_{n}(\xi )=\infty $
from some n onward.
The set of p-adic A-numbers coincides with the set of algebraic p-adic numbers. Therefore, the transcendental p-adic numbers are separated into the three disjoint classes S, T and U. If
![]() $\xi $
is a p-adic U-number and m is the minimum of the positive integers n satisfying
$\xi $
is a p-adic U-number and m is the minimum of the positive integers n satisfying
![]() $w_{n}(\xi )=\infty $
, then
$w_{n}(\xi )=\infty $
, then
![]() $\xi $
is called a p-adic
$\xi $
is called a p-adic
![]() $U_{m}$
-number. Alnıaçık [Reference Alnıaçık1, Ch. III, Theorem I] gave the first explicit constructions of p-adic
$U_{m}$
-number. Alnıaçık [Reference Alnıaçık1, Ch. III, Theorem I] gave the first explicit constructions of p-adic
![]() $U_{m}$
-numbers for each positive integer m. For further constructions of p-adic S-, T- and U-numbers, see [Reference Bugeaud and Kekeç4, Reference Bugeaud and Kekeç5, Reference Kekeç9, Reference Kekeç10].
$U_{m}$
-numbers for each positive integer m. For further constructions of p-adic S-, T- and U-numbers, see [Reference Bugeaud and Kekeç4, Reference Bugeaud and Kekeç5, Reference Kekeç9, Reference Kekeç10].
Assume that
![]() $\alpha $
is an algebraic p-adic number. Let
$\alpha $
is an algebraic p-adic number. Let
![]() $P(x)$
be the minimal polynomial of
$P(x)$
be the minimal polynomial of
![]() $\alpha $
over
$\alpha $
over
![]() $\mathbb {Z}$
. Then the degree
$\mathbb {Z}$
. Then the degree
![]() $\deg (\alpha )$
of
$\deg (\alpha )$
of
![]() $\alpha $
and the height
$\alpha $
and the height
![]() $H(\alpha )$
of
$H(\alpha )$
of
![]() $\alpha $
are defined by
$\alpha $
are defined by
![]() ${\deg (\alpha )=\deg (P)}$
and
${\deg (\alpha )=\deg (P)}$
and
![]() $H(\alpha )=H(P)$
. Given a p-adic number
$H(\alpha )=H(P)$
. Given a p-adic number
![]() $\xi $
and positive rational integers n, H, in analogy with Koksma’s classification [Reference Koksma12] of real numbers and as in Bugeaud [Reference Bugeaud3] and Schlickewei [Reference Schlickewei21]), set
$\xi $
and positive rational integers n, H, in analogy with Koksma’s classification [Reference Koksma12] of real numbers and as in Bugeaud [Reference Bugeaud3] and Schlickewei [Reference Schlickewei21]), set
 $$ \begin{align*} w_{n}^{*}(H, \xi)=\min\left\{|\xi-\alpha|_{p}:\! \begin{array}{ll} \alpha\textrm{ is an algebraic }p\textrm{-adic number},\\ \deg(\alpha)\leq n, H(\alpha)\leq H \textrm{ and } \alpha\neq\xi \end{array}\!\!\right\}, \end{align*} $$
$$ \begin{align*} w_{n}^{*}(H, \xi)=\min\left\{|\xi-\alpha|_{p}:\! \begin{array}{ll} \alpha\textrm{ is an algebraic }p\textrm{-adic number},\\ \deg(\alpha)\leq n, H(\alpha)\leq H \textrm{ and } \alpha\neq\xi \end{array}\!\!\right\}, \end{align*} $$
 $$ \begin{align*} w_{n}^{*}(\xi)=\limsup_{H \rightarrow \infty}\frac{-\log (H w_{n}^{*}(H, \xi))}{\log H} \quad \textrm{and} \quad w^{*}(\xi)=\limsup_{n \rightarrow \infty}\frac{w_{n}^{*}(\xi)}{n}. \end{align*} $$
$$ \begin{align*} w_{n}^{*}(\xi)=\limsup_{H \rightarrow \infty}\frac{-\log (H w_{n}^{*}(H, \xi))}{\log H} \quad \textrm{and} \quad w^{*}(\xi)=\limsup_{n \rightarrow \infty}\frac{w_{n}^{*}(\xi)}{n}. \end{align*} $$
Then
![]() $\xi $
is called:
$\xi $
is called:
-
• a p-adic
 $A^{*}$
-number if
$A^{*}$
-number if
 $w^{*}(\xi )=0$
;
$w^{*}(\xi )=0$
; -
• a p-adic
 $S^{*}$
-number if
$S^{*}$
-number if
 $0< w^{*}(\xi )<\infty $
;
$0< w^{*}(\xi )<\infty $
; -
• a p-adic
 $T^{*}$
-number if
$T^{*}$
-number if
 $w^{*}(\xi )=\infty $
and
$w^{*}(\xi )=\infty $
and
 $w_{n}^{*}(\xi )<\infty $
for
$w_{n}^{*}(\xi )<\infty $
for
 $n=1,2,3,\ldots $
; and
$n=1,2,3,\ldots $
; and -
• a p-adic
 $U^{*}$
-number if
$U^{*}$
-number if
 $w^{*}(\xi )=\infty $
and
$w^{*}(\xi )=\infty $
and
 $w_{n}^{*}(\xi )=\infty $
from some n onward.
$w_{n}^{*}(\xi )=\infty $
from some n onward.
The set of p-adic
![]() $A^{*}$
-numbers is equal to the set of algebraic p-adic numbers. Therefore, the transcendental p-adic numbers are separated into the three disjoint classes
$A^{*}$
-numbers is equal to the set of algebraic p-adic numbers. Therefore, the transcendental p-adic numbers are separated into the three disjoint classes
![]() $S^{*}$
,
$S^{*}$
,
![]() $T^{*}$
and
$T^{*}$
and
![]() $U^{*}$
. Let
$U^{*}$
. Let
![]() $\xi $
be a p-adic
$\xi $
be a p-adic
![]() $U^{*}$
-number and let m be the minimum of the positive integers n satisfying
$U^{*}$
-number and let m be the minimum of the positive integers n satisfying
![]() $w_{n}^{*}(\xi )=\infty $
. Then
$w_{n}^{*}(\xi )=\infty $
. Then
![]() $\xi $
is called a p-adic
$\xi $
is called a p-adic
![]() $U_{m}^{*}$
-number. Mahler’s classification of p-adic numbers is equivalent to Koksma’s classification of p-adic numbers, that is, the classes A, S, T and U are the same as the classes
$U_{m}^{*}$
-number. Mahler’s classification of p-adic numbers is equivalent to Koksma’s classification of p-adic numbers, that is, the classes A, S, T and U are the same as the classes
![]() $A^{*}$
,
$A^{*}$
,
![]() $S^{*}$
,
$S^{*}$
,
![]() $T^{*}$
and
$T^{*}$
and
![]() $U^{*}$
, respectively. Furthermore, a p-adic
$U^{*}$
, respectively. Furthermore, a p-adic
![]() $U_{m}^{*}$
-number is a p-adic
$U_{m}^{*}$
-number is a p-adic
![]() $U_{m}$
-number and vice versa. (See Bugeaud [Reference Bugeaud3] for further information on Mahler’s and Koksma’s classifications of p-adic numbers.)
$U_{m}$
-number and vice versa. (See Bugeaud [Reference Bugeaud3] for further information on Mahler’s and Koksma’s classifications of p-adic numbers.)
2. Ruban p-adic continued fractions
Ruban [Reference Ruban20] introduced a continued fraction algorithm in
![]() $\mathbb {Q}_{p}$
. In this section, we recall the Ruban p-adic continued fraction algorithm and its basic properties following the approach of Perron [Reference Perron19, Sections 29 and 30, pages 101–108] (see also [Reference Laohakosol14, Reference Ooto17, Reference Wang22, Reference Wang23]). Let
$\mathbb {Q}_{p}$
. In this section, we recall the Ruban p-adic continued fraction algorithm and its basic properties following the approach of Perron [Reference Perron19, Sections 29 and 30, pages 101–108] (see also [Reference Laohakosol14, Reference Ooto17, Reference Wang22, Reference Wang23]). Let
![]() $\xi $
be a nonzero p-adic number with the canonical expansion
$\xi $
be a nonzero p-adic number with the canonical expansion
 $$ \begin{align*} \xi=\sum_{j=k}^{\infty}a_{j}p^{j}, \end{align*} $$
$$ \begin{align*} \xi=\sum_{j=k}^{\infty}a_{j}p^{j}, \end{align*} $$
where
![]() $a_{j}\in \{0,1,\ldots ,p-1\}$
for
$a_{j}\in \{0,1,\ldots ,p-1\}$
for
![]() $j=k,k+1,\ldots , a_{k}\neq 0$
and k is the rational integer such that
$j=k,k+1,\ldots , a_{k}\neq 0$
and k is the rational integer such that
![]() $|\xi |_{p}=p^{-k}$
. If
$|\xi |_{p}=p^{-k}$
. If
![]() $k\leq 0$
, then we write
$k\leq 0$
, then we write
![]() $\xi =\{\xi \}+\lfloor \xi \rfloor $
, where
$\xi =\{\xi \}+\lfloor \xi \rfloor $
, where
 $$ \begin{align*} \{\xi\}=\sum_{j=k}^{0}a_{j}p^{j} \quad\textrm{and}\quad \lfloor\xi\rfloor=\sum_{j=1}^{\infty}a_{j}p^{j}. \end{align*} $$
$$ \begin{align*} \{\xi\}=\sum_{j=k}^{0}a_{j}p^{j} \quad\textrm{and}\quad \lfloor\xi\rfloor=\sum_{j=1}^{\infty}a_{j}p^{j}. \end{align*} $$
If
![]() $k>0$
, then we write
$k>0$
, then we write
![]() $\xi =\{\xi \}+\lfloor \xi \rfloor $
, where
$\xi =\{\xi \}+\lfloor \xi \rfloor $
, where
 $$ \begin{align*} \{\xi\}=0 \quad \textrm{and}\quad \lfloor\xi\rfloor=\sum_{j=k}^{\infty}a_{j}p^{j}. \end{align*} $$
$$ \begin{align*} \{\xi\}=0 \quad \textrm{and}\quad \lfloor\xi\rfloor=\sum_{j=k}^{\infty}a_{j}p^{j}. \end{align*} $$
Further, we write
![]() $0=\{0\}+\lfloor 0\rfloor $
, where
$0=\{0\}+\lfloor 0\rfloor $
, where
![]() $\{0\}=\lfloor 0\rfloor =0$
. Then, for each p-adic number
$\{0\}=\lfloor 0\rfloor =0$
. Then, for each p-adic number
![]() $\xi $
,
$\xi $
,
![]() $\{\xi \}$
and
$\{\xi \}$
and
![]() $\lfloor \xi \rfloor $
are uniquely determined. Let
$\lfloor \xi \rfloor $
are uniquely determined. Let
![]() $b_{0}, b_{1}, b_{2},\ldots $
be nonnegative rational numbers with
$b_{0}, b_{1}, b_{2},\ldots $
be nonnegative rational numbers with
A finite Ruban p-adic continued fraction
![]() $[b_{0}, b_{1},\ldots ,b_{n}]_{p}$
is defined by
$[b_{0}, b_{1},\ldots ,b_{n}]_{p}$
is defined by
 $$ \begin{align*} [b_0, b_1, \ldots, b_{n}]_{p}=b_0+\dfrac{1}{b_1+\dfrac{1}{\begin{array}{lr}\ddots\\ \qquad +\dfrac{1}{b_n}\end{array}}}. \end{align*} $$
$$ \begin{align*} [b_0, b_1, \ldots, b_{n}]_{p}=b_0+\dfrac{1}{b_1+\dfrac{1}{\begin{array}{lr}\ddots\\ \qquad +\dfrac{1}{b_n}\end{array}}}. \end{align*} $$
Then we have the following properties.
 $$ \begin{align*} [b_0, b_1, \ldots, b_{n}]_{p}=\bigg[b_0, b_1, \ldots, b_{n-2},b_{n-1}+\frac{1}{b_{n}}\bigg]_{p}=[b_0, b_1, \ldots, b_{m-1},[b_{m},\ldots,b_{n}]_{p}]_{p}, \end{align*} $$
$$ \begin{align*} [b_0, b_1, \ldots, b_{n}]_{p}=\bigg[b_0, b_1, \ldots, b_{n-2},b_{n-1}+\frac{1}{b_{n}}\bigg]_{p}=[b_0, b_1, \ldots, b_{m-1},[b_{m},\ldots,b_{n}]_{p}]_{p}, \end{align*} $$
 $$ \begin{align*} [b_0, b_1, \ldots, b_{n}]_{p}=b_{0}+\frac{1}{[b_1, \ldots, b_{n}]_{p}}. \end{align*} $$
$$ \begin{align*} [b_0, b_1, \ldots, b_{n}]_{p}=b_{0}+\frac{1}{[b_1, \ldots, b_{n}]_{p}}. \end{align*} $$
Hence,
![]() $[b_0, b_1, \ldots , b_{n}]_{p}$
is a nonnegative rational number, and the numbers
$[b_0, b_1, \ldots , b_{n}]_{p}$
is a nonnegative rational number, and the numbers
![]() ${b_{\nu}\ (\nu =0,1,\ldots ,n)}$
are called the partial quotients of the Ruban p-adic continued fraction
${b_{\nu}\ (\nu =0,1,\ldots ,n)}$
are called the partial quotients of the Ruban p-adic continued fraction
![]() $[b_0, b_1, \ldots , b_{n}]_{p}$
. Define the nonnegative rational numbers
$[b_0, b_1, \ldots , b_{n}]_{p}$
. Define the nonnegative rational numbers
![]() $p_{\nu }$
and
$p_{\nu }$
and
![]() $q_{\nu }$
by
$q_{\nu }$
by
 $$ \begin{align} \begin{cases}p_{-2}=0, \quad p_{-1}=1, \quad p_{\nu}=b_{\nu}p_{\nu-1}+p_{\nu-2} & (\nu=0,1,2,\ldots), \\ q_{-2}=1, \quad q_{-1}=0, \quad q_{\nu}=b_{\nu}q_{\nu-1}+q_{\nu-2} &(\nu=0,1,2,\ldots). \end{cases} \end{align} $$
$$ \begin{align} \begin{cases}p_{-2}=0, \quad p_{-1}=1, \quad p_{\nu}=b_{\nu}p_{\nu-1}+p_{\nu-2} & (\nu=0,1,2,\ldots), \\ q_{-2}=1, \quad q_{-1}=0, \quad q_{\nu}=b_{\nu}q_{\nu-1}+q_{\nu-2} &(\nu=0,1,2,\ldots). \end{cases} \end{align} $$
By induction,
The nonnegative rational numbers
![]() $p_{0}/q_{0}, p_{1}/q_{1},\ldots ,p_{n}/q_{n}$
are called the convergents of the Ruban p-adic continued fraction
$p_{0}/q_{0}, p_{1}/q_{1},\ldots ,p_{n}/q_{n}$
are called the convergents of the Ruban p-adic continued fraction
![]() $[b_0, b_1, \ldots , b_{n}]_{p}$
;
$[b_0, b_1, \ldots , b_{n}]_{p}$
;
![]() $p_{\nu }/q_{\nu }\ (\nu =0,1,\ldots ,n)$
is called the
$p_{\nu }/q_{\nu }\ (\nu =0,1,\ldots ,n)$
is called the
![]() $\nu $
th convergent of
$\nu $
th convergent of
![]() $[b_0, b_1, \ldots , b_{n}]_{p}$
. By induction,
$[b_0, b_1, \ldots , b_{n}]_{p}$
. By induction,
From (2.1),
for
![]() $n\kern1.4pt{=}\kern1.4pt 1,2,3,\ldots .$
As
$n\kern1.4pt{=}\kern1.4pt 1,2,3,\ldots .$
As
![]() $|b_{\nu }|_{p}\kern1.4pt{\geq}\kern1.4pt p\ (\nu =1,2,3,\ldots )$
, we have
$|b_{\nu }|_{p}\kern1.4pt{\geq}\kern1.4pt p\ (\nu =1,2,3,\ldots )$
, we have
![]() $|q_{n+1}|_{p}\kern1.4pt{>}\kern1.4pt|q_{n}|_{p}$
and
$|q_{n+1}|_{p}\kern1.4pt{>}\kern1.4pt|q_{n}|_{p}$
and
![]() ${|p_{n+1}|_{p}\kern1.4pt{>}\kern1.4pt|p_{n}|_{p}}$
for
${|p_{n+1}|_{p}\kern1.4pt{>}\kern1.4pt|p_{n}|_{p}}$
for
![]() $n=1,2,3,\ldots .$
Therefore,
$n=1,2,3,\ldots .$
Therefore,
By (2.2),
 $$ \begin{align*} \bigg|\frac{p_{n}}{q_{n}}-\frac{p_{n-1}}{q_{n-1}}\bigg|_{p}=\frac{1}{|q_{n}|_{p}\cdot|q_{n-1}|_{p}} \quad (n=1,2,3,\ldots). \end{align*} $$
$$ \begin{align*} \bigg|\frac{p_{n}}{q_{n}}-\frac{p_{n-1}}{q_{n-1}}\bigg|_{p}=\frac{1}{|q_{n}|_{p}\cdot|q_{n-1}|_{p}} \quad (n=1,2,3,\ldots). \end{align*} $$
Then
 $$ \begin{align*} \lim_{n\rightarrow\infty}\bigg|\frac{p_{n}}{q_{n}}-\frac{p_{n-1}}{q_{n-1}}\bigg|_{p}=0. \end{align*} $$
$$ \begin{align*} \lim_{n\rightarrow\infty}\bigg|\frac{p_{n}}{q_{n}}-\frac{p_{n-1}}{q_{n-1}}\bigg|_{p}=0. \end{align*} $$
Thus,
![]() $\{p_{n}/q_{n}\}_{n=0}^{\infty }$
is a Cauchy sequence in
$\{p_{n}/q_{n}\}_{n=0}^{\infty }$
is a Cauchy sequence in
![]() $\mathbb {Q}_{p}$
and has a limit in
$\mathbb {Q}_{p}$
and has a limit in
![]() $\mathbb {Q}_{p}$
. An infinite Ruban p-adic continued fraction
$\mathbb {Q}_{p}$
. An infinite Ruban p-adic continued fraction
![]() $[b_0, b_1, b_2, \ldots ]_{p}$
is defined as the limit of the sequence
$[b_0, b_1, b_2, \ldots ]_{p}$
is defined as the limit of the sequence
![]() $\{p_{n}/q_{n}\}_{n=0}^{\infty }$
, that is,
$\{p_{n}/q_{n}\}_{n=0}^{\infty }$
, that is,
Further, for
![]() $\xi \in \mathbb {Q}_{p}\setminus \{0\}$
,
$\xi \in \mathbb {Q}_{p}\setminus \{0\}$
,
Let
![]() $\xi _{0}$
be a p-adic number. If
$\xi _{0}$
be a p-adic number. If
![]() $\xi _{0}\neq \{\xi _{0}\}$
, then we write
$\xi _{0}\neq \{\xi _{0}\}$
, then we write
 $$ \begin{align*} \xi_{0}=b_{0}+\frac{1}{\xi_{1}}, \end{align*} $$
$$ \begin{align*} \xi_{0}=b_{0}+\frac{1}{\xi_{1}}, \end{align*} $$
where
![]() $b_{0}=\{\xi _{0}\}$
,
$b_{0}=\{\xi _{0}\}$
,
![]() $\xi _{1}=1/\lfloor \xi _{0}\rfloor $
,
$\xi _{1}=1/\lfloor \xi _{0}\rfloor $
,
![]() $|\xi _{1}|_{p}\geq p$
and
$|\xi _{1}|_{p}\geq p$
and
![]() $\{\xi _{1}\}\neq 0$
. If
$\{\xi _{1}\}\neq 0$
. If
![]() $\xi _{1}\neq \{\xi _{1}\}$
, then we write
$\xi _{1}\neq \{\xi _{1}\}$
, then we write
 $$ \begin{align*} \xi_{1}=b_{1}+\frac{1}{\xi_{2}}, \end{align*} $$
$$ \begin{align*} \xi_{1}=b_{1}+\frac{1}{\xi_{2}}, \end{align*} $$
where
![]() $b_{1}=\{\xi _{1}\}$
,
$b_{1}=\{\xi _{1}\}$
,
![]() $\xi _{2}=1/\lfloor \xi _{1}\rfloor $
,
$\xi _{2}=1/\lfloor \xi _{1}\rfloor $
,
![]() $|\xi _{2}|_{p}\geq p$
and
$|\xi _{2}|_{p}\geq p$
and
![]() $\{\xi _{2}\}\neq 0$
. If the process continues, then
$\{\xi _{2}\}\neq 0$
. If the process continues, then
 $$ \begin{align} \xi_{\nu}=b_{\nu}+\frac{1}{\xi_{\nu+1}} \quad (\nu\geq0), \end{align} $$
$$ \begin{align} \xi_{\nu}=b_{\nu}+\frac{1}{\xi_{\nu+1}} \quad (\nu\geq0), \end{align} $$
where
![]() $b_{\nu }=\{\xi _{\nu }\}\ (\nu \geq 0)$
and
$b_{\nu }=\{\xi _{\nu }\}\ (\nu \geq 0)$
and
![]() $\xi _{\nu +1}=1/\lfloor \xi _{\nu }\rfloor\ (\nu \geq 0)$
, and
$\xi _{\nu +1}=1/\lfloor \xi _{\nu }\rfloor\ (\nu \geq 0)$
, and
The p-adic numbers
![]() $\xi _{1}, \xi _{2},\ldots $
are called complete quotients, and the nonnegative rational numbers
$\xi _{1}, \xi _{2},\ldots $
are called complete quotients, and the nonnegative rational numbers
![]() $b_{0}, b_{1}, b_{2},\ldots $
are called partial quotients. It follows from (2.4) that
$b_{0}, b_{1}, b_{2},\ldots $
are called partial quotients. It follows from (2.4) that
and
 $$ \begin{align*} \xi_{0}-\frac{p_{n}}{q_{n}}=\frac{p_{n}\xi_{n+1}+p_{n-1}}{q_{n}\xi_{n+1}+q_{n-1}}-\frac{p_{n}}{q_{n}}=\frac{(-1)^{n}}{q_{n}(q_{n}\xi_{n+1}+q_{n-1})}. \end{align*} $$
$$ \begin{align*} \xi_{0}-\frac{p_{n}}{q_{n}}=\frac{p_{n}\xi_{n+1}+p_{n-1}}{q_{n}\xi_{n+1}+q_{n-1}}-\frac{p_{n}}{q_{n}}=\frac{(-1)^{n}}{q_{n}(q_{n}\xi_{n+1}+q_{n-1})}. \end{align*} $$
Then
 $$ \begin{align} \bigg|\xi_{0}-\frac{p_{n}}{q_{n}}\bigg|_{p}=\frac{1}{|\xi_{n+1}|_{p}\cdot|q_{n}|_{p}^{2}}=\frac{1}{|b_{n+1}|_{p}\cdot|q_{n}|_{p}^{2}}=\frac{1}{|q_{n+1}|_{p}\cdot|q_{n}|_{p}}<\frac{1}{|q_{n}|_{p}^{2}}. \end{align} $$
$$ \begin{align} \bigg|\xi_{0}-\frac{p_{n}}{q_{n}}\bigg|_{p}=\frac{1}{|\xi_{n+1}|_{p}\cdot|q_{n}|_{p}^{2}}=\frac{1}{|b_{n+1}|_{p}\cdot|q_{n}|_{p}^{2}}=\frac{1}{|q_{n+1}|_{p}\cdot|q_{n}|_{p}}<\frac{1}{|q_{n}|_{p}^{2}}. \end{align} $$
We now have two cases to consider.
Case (i). Some
![]() $\xi _{n+1}$
appears with
$\xi _{n+1}$
appears with
![]() $\xi _{n+1}=\{\xi _{n+1}\}=b_{n+1}$
and the process stops with
$\xi _{n+1}=\{\xi _{n+1}\}=b_{n+1}$
and the process stops with
![]() $\xi _{n+1}=b_{n+1}$
. Then it follows from (2.5) that
$\xi _{n+1}=b_{n+1}$
. Then it follows from (2.5) that
Case (ii).
![]() $\xi _{n+1}\neq \{\xi _{n+1}\}$
for every
$\xi _{n+1}\neq \{\xi _{n+1}\}$
for every
![]() $n\geq -1$
and the process never stops. Then it follows from (2.6) that
$n\geq -1$
and the process never stops. Then it follows from (2.6) that
The Ruban continued fraction expansion of a p-adic number is unique because the canonical expansion of a p-adic number is unique. Laohakosol [Reference Laohakosol14] and Wang [Reference Wang22] proved that a p-adic number is rational if and only if its Ruban continued fraction expansion is finite or ultimately periodic with the period
![]() $p-p^{-1}$
. Ooto [Reference Ooto17] recently proved that an analogue of Lagrange’s theorem does not hold for the Ruban p-adic continued fraction: that is, there are quadratic irrational p-adic numbers whose Ruban continued fraction expansions are not ultimately periodic.
$p-p^{-1}$
. Ooto [Reference Ooto17] recently proved that an analogue of Lagrange’s theorem does not hold for the Ruban p-adic continued fraction: that is, there are quadratic irrational p-adic numbers whose Ruban continued fraction expansions are not ultimately periodic.
3. Our main results
Alnıaçık [Reference Alnıaçık2, Theorem] gave a construction of real
![]() $U_{m}$
-numbers by using continued fraction expansions of algebraic irrational real numbers of degree m. In the present paper, we establish the following p-adic analogue.
$U_{m}$
-numbers by using continued fraction expansions of algebraic irrational real numbers of degree m. In the present paper, we establish the following p-adic analogue.
Theorem 3.1. Let
![]() $\alpha $
be an algebraic irrational p-adic number with
$\alpha $
be an algebraic irrational p-adic number with
![]() $|\alpha |_{p}\geq 1$
and the Ruban p-adic continued fraction expansion
$|\alpha |_{p}\geq 1$
and the Ruban p-adic continued fraction expansion
Let
![]() $(r_{n})_{n=0}^{\infty }$
and
$(r_{n})_{n=0}^{\infty }$
and
![]() $(s_{n})_{n=0}^{\infty }$
be two infinite sequences of nonnegative rational integers such that
$(s_{n})_{n=0}^{\infty }$
be two infinite sequences of nonnegative rational integers such that
Denote by
![]() $p_{n}/q_{n}\ (n=0,1,2,\ldots )$
the nth convergent of the Ruban p-adic continued fraction (3.1). Assume that
$p_{n}/q_{n}\ (n=0,1,2,\ldots )$
the nth convergent of the Ruban p-adic continued fraction (3.1). Assume that
 $$ \begin{align} \lim_{n \rightarrow \infty}\frac{\log |q_{s_{n}}|_{p}}{\log |q_{r_{n}}|_{p}}=\infty \end{align} $$
$$ \begin{align} \lim_{n \rightarrow \infty}\frac{\log |q_{s_{n}}|_{p}}{\log |q_{r_{n}}|_{p}}=\infty \end{align} $$
and
 $$ \begin{align} \limsup_{n \rightarrow \infty}\frac{\log |q_{r_{n+1}}|_{p}}{\log |q_{s_{n}}|_{p}}<\infty. \end{align} $$
$$ \begin{align} \limsup_{n \rightarrow \infty}\frac{\log |q_{r_{n+1}}|_{p}}{\log |q_{s_{n}}|_{p}}<\infty. \end{align} $$
Define the rational numbers
![]() $b_{j}\, (j=0,1,2,\ldots )$
by
$b_{j}\, (j=0,1,2,\ldots )$
by
 $$ \begin{align} b_{j}=\begin{cases}a_{j} \quad \mbox{if }r_{n}\leq j\leq s_{n} & (n=0,1,2,\ldots), \\ \upsilon_{j} \quad \mbox{if }s_{n}<j<r_{n+1} & (n=0,1,2,\ldots), \end{cases} \end{align} $$
$$ \begin{align} b_{j}=\begin{cases}a_{j} \quad \mbox{if }r_{n}\leq j\leq s_{n} & (n=0,1,2,\ldots), \\ \upsilon_{j} \quad \mbox{if }s_{n}<j<r_{n+1} & (n=0,1,2,\ldots), \end{cases} \end{align} $$
where
![]() $\upsilon _{j}$
is a rational number of the form
$\upsilon _{j}$
is a rational number of the form
Here,
![]() $d\in \mathbb {Z}$
,
$d\in \mathbb {Z}$
,
![]() $d>0$
,
$d>0$
,
![]() $c_{-d}\neq 0$
and
$c_{-d}\neq 0$
and
![]() $c_{i}\in \{0,1,\ldots ,p-1\}$
for
$c_{i}\in \{0,1,\ldots ,p-1\}$
for
![]() $i=-d, -d+1,\ldots , -1, 0$
. Note that
$i=-d, -d+1,\ldots , -1, 0$
. Note that
![]() $|\upsilon _{j}|_{p}\geq p$
. Suppose that
$|\upsilon _{j}|_{p}\geq p$
. Suppose that
![]() $|\upsilon _{j}|_{p}\leq \kappa _{1}|a_{j}|_{p}^{\kappa _{2}}$
and
$|\upsilon _{j}|_{p}\leq \kappa _{1}|a_{j}|_{p}^{\kappa _{2}}$
and
![]() $\sum _{j=s_{n}+1}^{r_{n+1}-1}|a_{j}-\upsilon _{j}|_{p}\neq 0$
, where
$\sum _{j=s_{n}+1}^{r_{n+1}-1}|a_{j}-\upsilon _{j}|_{p}\neq 0$
, where
![]() $\kappa _{1}$
and
$\kappa _{1}$
and
![]() $\kappa _{2}$
are fixed positive rational integers. Then the irrational p-adic number
$\kappa _{2}$
are fixed positive rational integers. Then the irrational p-adic number
![]() ${\xi =[b_0,b_1,b_2,\ldots ]_{p}}$
is a p-adic
${\xi =[b_0,b_1,b_2,\ldots ]_{p}}$
is a p-adic
![]() $U_{m}$
-number, where m denotes the degree of the algebraic irrational p-adic number
$U_{m}$
-number, where m denotes the degree of the algebraic irrational p-adic number
![]() $\alpha $
.
$\alpha $
.
Remark 3.2. Let
![]() $\mathbb {F}_{q}$
be the finite field with q elements and let
$\mathbb {F}_{q}$
be the finite field with q elements and let
![]() $\mathbb {F}_{q}((x^{-1}))$
be the field of formal power series over
$\mathbb {F}_{q}((x^{-1}))$
be the field of formal power series over
![]() $\mathbb {F}_{q}$
. In
$\mathbb {F}_{q}$
. In
![]() $\mathbb {F}_{q}((x^{-1}))$
, Can and Kekeç [Reference Can and Kekeç6, Theorem 1.1] recently established the formal power series analogue of Alnıaçık [Reference Alnıaçık2, Theorem].
$\mathbb {F}_{q}((x^{-1}))$
, Can and Kekeç [Reference Can and Kekeç6, Theorem 1.1] recently established the formal power series analogue of Alnıaçık [Reference Alnıaçık2, Theorem].
Recently, Kekeç [Reference Kekeç11, Theorem 1.5] modified the hypotheses in Alnıaçık [Reference Alnıaçık2, Theorem] and gave a construction of transcendental real numbers that are not U-numbers by using continued fraction expansions of irrational algebraic real numbers. Our second main result in the present paper is the following partial p-adic analogue of Kekeç [Reference Kekeç11, Theorem 1.5].
Theorem 3.3. Let
![]() $\alpha $
be an algebraic p-adic number of degree
$\alpha $
be an algebraic p-adic number of degree
![]() $m\geq 2$
with
$m\geq 2$
with
![]() $|\alpha |_{p}\geq 1$
and the Ruban p-adic continued fraction expansion
$|\alpha |_{p}\geq 1$
and the Ruban p-adic continued fraction expansion
Let
![]() $(r_{n})_{n=0}^{\infty }$
and
$(r_{n})_{n=0}^{\infty }$
and
![]() $(s_{n})_{n=0}^{\infty }$
be two infinite sequences of nonnegative rational integers such that
$(s_{n})_{n=0}^{\infty }$
be two infinite sequences of nonnegative rational integers such that
Denote by
![]() $p_{n}/q_{n}\ (n=0,1,2,\ldots )$
the nth convergent of the Ruban p-adic continued fraction
$p_{n}/q_{n}\ (n=0,1,2,\ldots )$
the nth convergent of the Ruban p-adic continued fraction
![]() $\alpha $
. Define the rational numbers
$\alpha $
. Define the rational numbers
![]() $b_{\,j}\ (j=0,1,2,\ldots )$
by
$b_{\,j}\ (j=0,1,2,\ldots )$
by
 $$ \begin{align} b_{j}= \begin{cases}a_{j} \quad \mbox{if }r_{n}\leq j\leq s_{n} & (n=0,1,2,\ldots), \\ \upsilon_{j} \quad \mbox{if }s_{n}<j<r_{n+1} & (n=0,1,2,\ldots), \end{cases} \end{align} $$
$$ \begin{align} b_{j}= \begin{cases}a_{j} \quad \mbox{if }r_{n}\leq j\leq s_{n} & (n=0,1,2,\ldots), \\ \upsilon_{j} \quad \mbox{if }s_{n}<j<r_{n+1} & (n=0,1,2,\ldots), \end{cases} \end{align} $$
where
![]() $\upsilon _{j}$
is a rational number of the form
$\upsilon _{j}$
is a rational number of the form
Here
![]() $d\in \mathbb {Z}$
,
$d\in \mathbb {Z}$
,
![]() $d>0$
,
$d>0$
,
![]() $c_{-d}\neq 0$
and
$c_{-d}\neq 0$
and
![]() $c_{i}\in \{0,1,\ldots ,p-1\}$
for
$c_{i}\in \{0,1,\ldots ,p-1\}$
for
![]() $i=-d, -d+1,\ldots , -1, 0$
. Note that
$i=-d, -d+1,\ldots , -1, 0$
. Note that
![]() $|\upsilon _{j}|_{p}\geq p$
. Suppose that
$|\upsilon _{j}|_{p}\geq p$
. Suppose that
![]() $|\upsilon _{j}|_{p}\leq \kappa _{1}|a_{j}|_{p}^{\kappa _{2}}$
and
$|\upsilon _{j}|_{p}\leq \kappa _{1}|a_{j}|_{p}^{\kappa _{2}}$
and
![]() $\sum _{j=s_{n}+1}^{r_{n+1}-1}|a_{j}-\upsilon _{j}|_{p}\neq 0$
, where
$\sum _{j=s_{n}+1}^{r_{n+1}-1}|a_{j}-\upsilon _{j}|_{p}\neq 0$
, where
![]() $\kappa _{1}$
and
$\kappa _{1}$
and
![]() $\kappa _{2}$
are fixed positive rational integers. Assume that
$\kappa _{2}$
are fixed positive rational integers. Assume that
 $$ \begin{align} \liminf_{n \rightarrow \infty}\frac{\log |q_{s_{n}}|_{p}}{\log |q_{r_{n}}|_{p}}>2+4m\bigg(m+\kappa_{2}+\frac{\log \kappa_{1}}{\log 2}\bigg). \end{align} $$
$$ \begin{align} \liminf_{n \rightarrow \infty}\frac{\log |q_{s_{n}}|_{p}}{\log |q_{r_{n}}|_{p}}>2+4m\bigg(m+\kappa_{2}+\frac{\log \kappa_{1}}{\log 2}\bigg). \end{align} $$
Then the irrational p-adic number
![]() $\xi =[b_0,b_1,b_2,\ldots ]_{p}$
is transcendental.
$\xi =[b_0,b_1,b_2,\ldots ]_{p}$
is transcendental.
In the next section, we cite some auxiliary results that we need to prove our results. In Section 5, we prove Theorems 3.1 and 3.3.
4. Auxiliary results
The following lemma is a p-adic analogue of Alnıaçık [Reference Alnıaçık2, Lemma IV].
Lemma 4.1. Let
![]() $p/q$
and
$p/q$
and
![]() $u/v$
be two rational numbers with Ruban p-adic continued fraction expansions
$u/v$
be two rational numbers with Ruban p-adic continued fraction expansions
Assume that
where
![]() $\kappa _{1}$
and
$\kappa _{1}$
and
![]() $\kappa _{2}$
are fixed positive rational integers. Then
$\kappa _{2}$
are fixed positive rational integers. Then
Proof. It follows from (4.1) that
As
![]() $|q|_{p}=|a_{1}|_{p}\cdots |a_{n}|_{p}\geq p^{n}\geq 2^{n}$
,
$|q|_{p}=|a_{1}|_{p}\cdots |a_{n}|_{p}\geq p^{n}\geq 2^{n}$
,
Theorem 4.2 (Içen [Reference İçen8, page 25] and [Reference İçen7, Lemma 1, page 71]).
Let L be a p-adic algebraic number field of degree m and let
![]() $\alpha _1,\ldots ,\alpha _k$
be algebraic p-adic numbers in L. Let
$\alpha _1,\ldots ,\alpha _k$
be algebraic p-adic numbers in L. Let
![]() $\eta $
be any algebraic p-adic number. Suppose that
$\eta $
be any algebraic p-adic number. Suppose that
![]() $F(\eta ,\alpha _1,\ldots ,\alpha _k)=0$
, where
$F(\eta ,\alpha _1,\ldots ,\alpha _k)=0$
, where
![]() $F(x,x_1,\ldots ,x_k)$
is a polynomial in
$F(x,x_1,\ldots ,x_k)$
is a polynomial in
![]() $x, x_{1},\ldots ,x_{k}$
over
$x, x_{1},\ldots ,x_{k}$
over
![]() $\mathbb {Z}$
with degree at least one in x. Then
$\mathbb {Z}$
with degree at least one in x. Then
where d is the degree of
![]() $F(x,x_1,\ldots ,x_k)$
in x,
$F(x,x_1,\ldots ,x_k)$
in x,
![]() $l_i$
is the degree of
$l_i$
is the degree of
![]() $F(x,x_1,\ldots ,x_k)$
in
$F(x,x_1,\ldots ,x_k)$
in
![]() ${x_i\ (i=1,\ldots ,k)}$
and H is the maximum of the usual absolute values of the coefficients of
${x_i\ (i=1,\ldots ,k)}$
and H is the maximum of the usual absolute values of the coefficients of
![]() $F(x,x_1,\ldots ,x_k)$
.
$F(x,x_1,\ldots ,x_k)$
.
Lemma 4.3 (Pejkovic [Reference Pejkovic18, Lemma 2.5]).
Let
![]() $\alpha _{1}$
and
$\alpha _{1}$
and
![]() $\alpha _{2}$
be two distinct algebraic p-adic numbers. Then
$\alpha _{2}$
be two distinct algebraic p-adic numbers. Then
Lemma 4.4 (Ooto [Reference Ooto17, Lemma 7 and page 1058]).
Let
![]() $\alpha $
be a p-adic number with
$\alpha $
be a p-adic number with
![]() $|\alpha |_{p}\geq 1$
and let
$|\alpha |_{p}\geq 1$
and let
![]() $p_{n}/q_{n}$
be the nth convergent of its Ruban p-adic continued fraction expansion. Then
$p_{n}/q_{n}$
be the nth convergent of its Ruban p-adic continued fraction expansion. Then
![]() $p_{n}\leq |p_{n}|_{p}$
,
$p_{n}\leq |p_{n}|_{p}$
,
![]() $q_{n}\leq |q_{n}|_{p}$
and
$q_{n}\leq |q_{n}|_{p}$
and
Theorem 4.5 (Lang [Reference Lang13, page 32]).
Let K be a p-adic algebraic number field and let
![]() $\alpha $
be any algebraic p-adic number. Then, for each
$\alpha $
be any algebraic p-adic number. Then, for each
![]() $\varepsilon>0$
, the inequality
$\varepsilon>0$
, the inequality
 $$ \begin{align*} |\alpha-\beta|_{p}<\frac{1}{H(\beta)^{2+\varepsilon}} \end{align*} $$
$$ \begin{align*} |\alpha-\beta|_{p}<\frac{1}{H(\beta)^{2+\varepsilon}} \end{align*} $$
has only finitely many solutions
![]() $\beta $
in K.
$\beta $
in K.
5. Proofs of Theorems 3.1 and 3.3
Proof of Theorem 3.1.
We prove Theorem 3.1 by adapting the method of the proof of Alnıaçık [Reference Alnıaçık2, Theorem] to the non-Archimedean p-adic case. Define the algebraic p-adic numbers
and
Then
![]() $\deg (\alpha _{r_{n}})=\deg (\beta _{r_{n}})=m\ (n=0,1,2,\ldots )$
. By (2.3),
$\deg (\alpha _{r_{n}})=\deg (\beta _{r_{n}})=m\ (n=0,1,2,\ldots )$
. By (2.3),
 $$ \begin{align*} \alpha=[a_{0}, a_{1},\ldots,a_{r_{n}},\beta_{r_{n}}]_{p}=\frac{p_{r_{n}}\beta_{r_{n}}+p_{r_{n}-1}}{q_{r_{n}}\beta_{r_{n}}+q_{r_{n}-1}} \quad (n=0,1,2,\ldots) \end{align*} $$
$$ \begin{align*} \alpha=[a_{0}, a_{1},\ldots,a_{r_{n}},\beta_{r_{n}}]_{p}=\frac{p_{r_{n}}\beta_{r_{n}}+p_{r_{n}-1}}{q_{r_{n}}\beta_{r_{n}}+q_{r_{n}-1}} \quad (n=0,1,2,\ldots) \end{align*} $$
and thus
Therefore,
![]() $F(\beta _{r_{n}}, \alpha )=0$
, where, by Lemma 4.4,
$F(\beta _{r_{n}}, \alpha )=0$
, where, by Lemma 4.4,
is a polynomial in
![]() $x, x_{1}$
over
$x, x_{1}$
over
![]() $\mathbb {Z}$
. It follows from Theorem 4.2 and Lemma 4.4 that
$\mathbb {Z}$
. It follows from Theorem 4.2 and Lemma 4.4 that
where
![]() $c_{1}=3^{3m}|a_{0}|_{p}^{2m}H(\alpha )^{m}$
. Set
$c_{1}=3^{3m}|a_{0}|_{p}^{2m}H(\alpha )^{m}$
. Set
 $$ \begin{align*} \frac{p_{n}'}{q_{n}'}:=[b_{0}, b_{1},\ldots,b_{n}]_{p} \quad (n=0,1,2,\ldots). \end{align*} $$
$$ \begin{align*} \frac{p_{n}'}{q_{n}'}:=[b_{0}, b_{1},\ldots,b_{n}]_{p} \quad (n=0,1,2,\ldots). \end{align*} $$
Then
 $$ \begin{align*} \alpha_{r_{n}}=[b_{0}, b_{1},\ldots,b_{r_{n}},\beta_{r_{n}}]_{p}=\frac{p_{r_{n}}'\beta_{r_{n}}+p_{r_{n}-1}'}{q_{r_{n}}'\beta_{r_{n}}+q_{r_{n}-1}'} \quad (n=0,1,2,\ldots) \end{align*} $$
$$ \begin{align*} \alpha_{r_{n}}=[b_{0}, b_{1},\ldots,b_{r_{n}},\beta_{r_{n}}]_{p}=\frac{p_{r_{n}}'\beta_{r_{n}}+p_{r_{n}-1}'}{q_{r_{n}}'\beta_{r_{n}}+q_{r_{n}-1}'} \quad (n=0,1,2,\ldots) \end{align*} $$
and
Thus,
![]() $F(\alpha _{r_{n}}, \beta _{r_{n}})=0$
, where, by Lemma 4.4,
$F(\alpha _{r_{n}}, \beta _{r_{n}})=0$
, where, by Lemma 4.4,
is a polynomial in
![]() $x, x_{1}$
over
$x, x_{1}$
over
![]() $\mathbb {Z}$
. It follows from Theorem 4.2, Lemma 4.4 and (5.1) that
$\mathbb {Z}$
. It follows from Theorem 4.2, Lemma 4.4 and (5.1) that
From (3.4),
By Lemma 4.1,
Using (5.2), (5.3) and
![]() $\lim _{n \rightarrow \infty } |q_{r_{n}}|_{p}=\infty $
, we obtain, for sufficiently large n,
$\lim _{n \rightarrow \infty } |q_{r_{n}}|_{p}=\infty $
, we obtain, for sufficiently large n,
where
![]() $c_{2}=1+(m+\kappa _{2}+\log \kappa _{1}{/}\kern-1.2pt\log 2)2m$
.
$c_{2}=1+(m+\kappa _{2}+\log \kappa _{1}{/}\kern-1.2pt\log 2)2m$
.
We approximate
![]() $\xi $
by the algebraic p-adic numbers
$\xi $
by the algebraic p-adic numbers
![]() $\alpha _{r_{n}}$
. We infer from (2.6) and (3.4) that
$\alpha _{r_{n}}$
. We infer from (2.6) and (3.4) that
 $$ \begin{align} |\xi-\alpha_{r_{n}}|_{p}\leq \max \bigg\{\bigg|\xi-\frac{p_{s_{n}}'}{q_{s_{n}}'}\bigg|_{p}, \bigg|\alpha_{r_{n}}-\frac{p_{s_{n}}'}{q_{s_{n}}'}\bigg|_{p}\bigg\}<\frac{1}{|q_{s_{n}}'|_{p}^{2}} \quad (n=0,1,2,\ldots). \end{align} $$
$$ \begin{align} |\xi-\alpha_{r_{n}}|_{p}\leq \max \bigg\{\bigg|\xi-\frac{p_{s_{n}}'}{q_{s_{n}}'}\bigg|_{p}, \bigg|\alpha_{r_{n}}-\frac{p_{s_{n}}'}{q_{s_{n}}'}\bigg|_{p}\bigg\}<\frac{1}{|q_{s_{n}}'|_{p}^{2}} \quad (n=0,1,2,\ldots). \end{align} $$
Put
 $$ \begin{align*} \frac{d_{r_{n}}}{e_{r_{n}}}:=[a_{r_{n}+1},a_{r_{n}+2},\ldots,a_{s_{n}}]_{p}=[b_{r_{n}+1},b_{r_{n}+2},\ldots,b_{s_{n}}]_{p}. \end{align*} $$
$$ \begin{align*} \frac{d_{r_{n}}}{e_{r_{n}}}:=[a_{r_{n}+1},a_{r_{n}+2},\ldots,a_{s_{n}}]_{p}=[b_{r_{n}+1},b_{r_{n}+2},\ldots,b_{s_{n}}]_{p}. \end{align*} $$
We have
and
 $$ \begin{align*} \frac{p_{s_{n}}'}{q_{s_{n}}'}=[b_{0},b_{1},\ldots,b_{r_{n}},b_{r_{n}+1},b_{r_{n}+2},\ldots,b_{s_{n}}]_{p}. \end{align*} $$
$$ \begin{align*} \frac{p_{s_{n}}'}{q_{s_{n}}'}=[b_{0},b_{1},\ldots,b_{r_{n}},b_{r_{n}+1},b_{r_{n}+2},\ldots,b_{s_{n}}]_{p}. \end{align*} $$
Then
and
Therefore,
It follows from Lemmas 4.3 and 4.4 that
 $$ \begin{align} \bigg|\alpha-\frac{p_{r_{n}}}{q_{r_{n}}}\bigg|_{p}\geq\frac{1}{c_{3}|q_{r_{n}}|_{p}^{2m}}, \end{align} $$
$$ \begin{align} \bigg|\alpha-\frac{p_{r_{n}}}{q_{r_{n}}}\bigg|_{p}\geq\frac{1}{c_{3}|q_{r_{n}}|_{p}^{2m}}, \end{align} $$
where
![]() $c_{3}=(m+1)2^{m}H(\alpha )|a_{0}|_{p}^{2m}$
. On the other hand, by (2.6),
$c_{3}=(m+1)2^{m}H(\alpha )|a_{0}|_{p}^{2m}$
. On the other hand, by (2.6),
 $$ \begin{align} \bigg|\alpha-\frac{p_{r_{n}}}{q_{r_{n}}}\bigg|_{p}=\frac{1}{|a_{r_{n}+1}|_{p}|q_{r_{n}}|_{p}^{2}} \quad (n=0,1,2,\ldots). \end{align} $$
$$ \begin{align} \bigg|\alpha-\frac{p_{r_{n}}}{q_{r_{n}}}\bigg|_{p}=\frac{1}{|a_{r_{n}+1}|_{p}|q_{r_{n}}|_{p}^{2}} \quad (n=0,1,2,\ldots). \end{align} $$
Combining (5.6), (5.7) and (5.8), we get
for sufficiently large n. So, for sufficiently large n,
We see from (3.2), (5.4), (5.5) and (5.10) that
 $$ \begin{align*} 0<|\xi-\alpha_{r_{n}}|_{p}<\frac{1}{|q_{s_{n}}|_{p}}\leq\frac{1}{H(\alpha_{r_{n}})^{\phi_{n}}} \end{align*} $$
$$ \begin{align*} 0<|\xi-\alpha_{r_{n}}|_{p}<\frac{1}{|q_{s_{n}}|_{p}}\leq\frac{1}{H(\alpha_{r_{n}})^{\phi_{n}}} \end{align*} $$
for sufficiently large n, where
 $$ \begin{align*} \phi_{n}=\frac{\log |q_{s_{n}}|_{p}}{c_{2}\log |q_{r_{n}}|_{p}} \hspace{0.15in} \textrm{and} \hspace{0.15in} \lim_{n \rightarrow \infty} \phi_{n}=\infty. \end{align*} $$
$$ \begin{align*} \phi_{n}=\frac{\log |q_{s_{n}}|_{p}}{c_{2}\log |q_{r_{n}}|_{p}} \hspace{0.15in} \textrm{and} \hspace{0.15in} \lim_{n \rightarrow \infty} \phi_{n}=\infty. \end{align*} $$
As
![]() $\deg (\alpha _{r_{n}})=m\ (n=0,1,2,\ldots )$
, this shows that
$\deg (\alpha _{r_{n}})=m\ (n=0,1,2,\ldots )$
, this shows that
![]() $\xi $
is a p-adic
$\xi $
is a p-adic
![]() $U^{*}$
-number with
$U^{*}$
-number with
We wish to show that
![]() $\xi $
is a p-adic
$\xi $
is a p-adic
![]() $U_{m}^{*}$
-number. We must prove that
$U_{m}^{*}$
-number. We must prove that
![]() $w_{t}^{*}(\xi )<\infty $
for
$w_{t}^{*}(\xi )<\infty $
for
![]() $t=1,\ldots ,m-1$
. Let
$t=1,\ldots ,m-1$
. Let
![]() $\beta $
be any algebraic p-adic number with
$\beta $
be any algebraic p-adic number with
![]() $1\leq \deg (\beta )\leq m-1$
and with sufficiently large height
$1\leq \deg (\beta )\leq m-1$
and with sufficiently large height
![]() $H(\beta )$
. We deduce from Lemma 4.3 and (5.4) that
$H(\beta )$
. We deduce from Lemma 4.3 and (5.4) that
 $$ \begin{align} |\alpha_{r_{n}}-\beta|_{p}\geq \frac{1}{c_{4}|q_{r_{n}}|_{p}^{c_{5}}H(\beta)^{m}} \end{align} $$
$$ \begin{align} |\alpha_{r_{n}}-\beta|_{p}\geq \frac{1}{c_{4}|q_{r_{n}}|_{p}^{c_{5}}H(\beta)^{m}} \end{align} $$
for sufficiently large n, where
![]() $c_{4}=(m+1)^{m-1}m^{m}$
and
$c_{4}=(m+1)^{m-1}m^{m}$
and
![]() $c_{5}=c_{2}(m-1)$
. By (3.3), there exists a real number
$c_{5}=c_{2}(m-1)$
. By (3.3), there exists a real number
![]() $T>1$
such that
$T>1$
such that
for sufficiently large n. We have
From (5.5), (5.10) and (5.13), for sufficiently large n,
 $$ \begin{align} |\xi-\alpha_{r_{n}}|_{p}<\frac{1}{|q_{s_{n}}'|_{p}^{2}}<\frac{1}{|q_{s_{n}}|_{p}}\leq\frac{1}{|q_{r_{n+1}}|_{p}^{1/T}}. \end{align} $$
$$ \begin{align} |\xi-\alpha_{r_{n}}|_{p}<\frac{1}{|q_{s_{n}}'|_{p}^{2}}<\frac{1}{|q_{s_{n}}|_{p}}\leq\frac{1}{|q_{r_{n+1}}|_{p}^{1/T}}. \end{align} $$
Let i be the unique positive rational integer satisfying
![]() $|q_{r_{i}}|_{p}\leq H(\beta )<|q_{r_{i+1}}|_{p}$
. Put
$|q_{r_{i}}|_{p}\leq H(\beta )<|q_{r_{i+1}}|_{p}$
. Put
![]() ${T_{1}:=T(m+c_{5}+1)}$
. If
${T_{1}:=T(m+c_{5}+1)}$
. If
![]() $|q_{r_{i}}|_{p}\leq H(\beta )<|q_{r_{i+1}}|_{p}^{1/T_{1}}$
, then it follows from (5.12), (5.14) and (5.15) with
$|q_{r_{i}}|_{p}\leq H(\beta )<|q_{r_{i+1}}|_{p}^{1/T_{1}}$
, then it follows from (5.12), (5.14) and (5.15) with
![]() $n=i$
that
$n=i$
that
 $$ \begin{align} |\xi-\beta|_{p}\geq \frac{1}{c_{4}H(\beta)^{m+c_{5}}}. \end{align} $$
$$ \begin{align} |\xi-\beta|_{p}\geq \frac{1}{c_{4}H(\beta)^{m+c_{5}}}. \end{align} $$
If
![]() $|q_{r_{i+1}}|_{p}^{1/T_{1}}\leq H(\beta )<|q_{r_{i+1}}|_{p}$
, then it follows from (3.2), (5.12), (5.14) and (5.15) with
$|q_{r_{i+1}}|_{p}^{1/T_{1}}\leq H(\beta )<|q_{r_{i+1}}|_{p}$
, then it follows from (3.2), (5.12), (5.14) and (5.15) with
![]() $n=i+1$
that
$n=i+1$
that
 $$ \begin{align} |\xi-\beta|_{p}\geq \frac{1}{c_{4}H(\beta)^{m+c_{5}T_{1}}}. \end{align} $$
$$ \begin{align} |\xi-\beta|_{p}\geq \frac{1}{c_{4}H(\beta)^{m+c_{5}T_{1}}}. \end{align} $$
We deduce from (5.16) and (5.17) that
 $$ \begin{align*} |\xi-\beta|_{p}\geq \frac{1}{c_{4}H(\beta)^{m+c_{5}T_{1}}} \end{align*} $$
$$ \begin{align*} |\xi-\beta|_{p}\geq \frac{1}{c_{4}H(\beta)^{m+c_{5}T_{1}}} \end{align*} $$
for all algebraic p-adic numbers
![]() $\beta $
with
$\beta $
with
![]() $\deg (\beta )\leq m-1$
and with sufficiently large height
$\deg (\beta )\leq m-1$
and with sufficiently large height
![]() $H(\beta )$
. This gives
$H(\beta )$
. This gives
We infer from (5.11) and (5.18) that
![]() $\xi $
is a p-adic
$\xi $
is a p-adic
![]() $U_{m}^{*}$
-number. As the set of p-adic
$U_{m}^{*}$
-number. As the set of p-adic
![]() $U_{m}$
-numbers is equal to the set of p-adic
$U_{m}$
-numbers is equal to the set of p-adic
![]() $U_{m}^{*}$
-numbers,
$U_{m}^{*}$
-numbers,
![]() $\xi $
is a p-adic
$\xi $
is a p-adic
![]() $U_{m}$
-number.
$U_{m}$
-number.
Example 5.1. This example illustrates Theorem 3.1. In Theorem 3.1, take the algebraic p-adic number
![]() $\alpha $
as the quadratic irrational
$\alpha $
as the quadratic irrational
and the sequences
![]() $(r_{n})_{n=0}^{\infty }$
and
$(r_{n})_{n=0}^{\infty }$
and
![]() $(s_{n})_{n=0}^{\infty }$
as
$(s_{n})_{n=0}^{\infty }$
as
Define the rational numbers
![]() $b_{j}\ (j=0,1,2,\ldots )$
by
$b_{j}\ (j=0,1,2,\ldots )$
by
 $$ \begin{align*} b_{j}= \begin{cases}p^{-2} \quad \mbox{if }r_{n}\leq j\leq s_{n} & (n=0,1,2,\ldots), \\ p^{-4} \quad \mbox{if }s_{n}<j<r_{n+1} & (n=0,1,2,\ldots). \end{cases} \end{align*} $$
$$ \begin{align*} b_{j}= \begin{cases}p^{-2} \quad \mbox{if }r_{n}\leq j\leq s_{n} & (n=0,1,2,\ldots), \\ p^{-4} \quad \mbox{if }s_{n}<j<r_{n+1} & (n=0,1,2,\ldots). \end{cases} \end{align*} $$
Take
![]() $\kappa _{1}=1$
and
$\kappa _{1}=1$
and
![]() $\kappa _{2}=2$
. Then all the conditions of Theorem 3.1 are satisfied and therefore the irrational p-adic number
$\kappa _{2}=2$
. Then all the conditions of Theorem 3.1 are satisfied and therefore the irrational p-adic number
![]() $\xi =[b_0,b_1,b_2,\ldots ]_{p}$
is a p-adic
$\xi =[b_0,b_1,b_2,\ldots ]_{p}$
is a p-adic
![]() $U_{2}$
-number.
$U_{2}$
-number.
Remark 5.2. In Theorem 3.1, if we replace
![]() $\lim _{n \rightarrow \infty }(\log |q_{s_{n}}|_{p}{/}\kern-1.2pt\log |q_{r_{n}}|_{p})=\infty $
by
$\lim _{n \rightarrow \infty }(\log |q_{s_{n}}|_{p}{/}\kern-1.2pt\log |q_{r_{n}}|_{p})=\infty $
by
 $$ \begin{align*} \liminf_{n \rightarrow \infty}\frac{\log |q_{s_{n}}|_{p}}{\log |q_{r_{n}}|_{p}}>T(1+m+c_{5}T_{1}) \quad \textrm{and} \quad \limsup_{n \rightarrow \infty}\frac{\log |q_{s_{n}}|_{p}}{\log |q_{r_{n}}|_{p}}=\infty, \end{align*} $$
$$ \begin{align*} \liminf_{n \rightarrow \infty}\frac{\log |q_{s_{n}}|_{p}}{\log |q_{r_{n}}|_{p}}>T(1+m+c_{5}T_{1}) \quad \textrm{and} \quad \limsup_{n \rightarrow \infty}\frac{\log |q_{s_{n}}|_{p}}{\log |q_{r_{n}}|_{p}}=\infty, \end{align*} $$
then we see from the proof that Theorem 3.1 still holds true.
Proof of Theorem 3.3.
We replace (3.2) by (3.6) and keep all the lines of the proof of Theorem 3.1 up to (5.10). By (3.6), there exists a positive real number
![]() $\varepsilon $
such that
$\varepsilon $
such that
 $$ \begin{align} \frac{\log |q_{s_{n}}|_{p}}{\log |q_{r_{n}}|_{p}}>(2+\varepsilon)c_{2} \end{align} $$
$$ \begin{align} \frac{\log |q_{s_{n}}|_{p}}{\log |q_{r_{n}}|_{p}}>(2+\varepsilon)c_{2} \end{align} $$
for sufficiently large n. We deduce from (5.4), (5.5), (5.10) and (5.19) that
 $$ \begin{align*} 0<|\xi-\alpha_{r_{n}}|_{p}<\frac{1}{H(\alpha_{r_{n}})^{2+\varepsilon}} \end{align*} $$
$$ \begin{align*} 0<|\xi-\alpha_{r_{n}}|_{p}<\frac{1}{H(\alpha_{r_{n}})^{2+\varepsilon}} \end{align*} $$
for sufficiently large n. It follows from the definition of
![]() $\alpha _{r_{n}}$
and (3.5) that the algebraic p-adic numbers
$\alpha _{r_{n}}$
and (3.5) that the algebraic p-adic numbers
![]() $\alpha _{r_{n}}$
in
$\alpha _{r_{n}}$
in
![]() $\mathbb {Q}(\alpha )$
are all distinct. Then, by Theorem 4.5, the irrational p-adic number
$\mathbb {Q}(\alpha )$
are all distinct. Then, by Theorem 4.5, the irrational p-adic number
![]() $\xi $
is transcendental.
$\xi $
is transcendental.
Finally, we pose the following question.
Problem 5.3. Does an exact analogue of Kekeç [Reference Kekeç11, Theorem 1.5] hold in
![]() $\mathbb {Q}_{p}$
?
$\mathbb {Q}_{p}$
?