Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T08:08:57.218Z Has data issue: false hasContentIssue false
  • English
  • Français

TOUGHNESS, ISOLATED TOUGHNESS AND PATH FACTORS IN GRAPHS

Part of: Graph theory

Published online by Cambridge University Press:  03 December 2021

SIZHONG ZHOU Open the ORCID record for SIZHONG ZHOU [Opens in a new window] ,
JIANCHENG WU  and
YANG XU
SIZHONG ZHOU*
Affiliation:
School of Science, Jiangsu University of Science and Technology, Zhenjiang, Jiangsu 212100, China
JIANCHENG WU
Affiliation:
School of Science, Jiangsu University of Science and Technology, Zhenjiang, Jiangsu 212100, China e-mail: [email protected]
YANG XU
Affiliation:
Department of Mathematics, Qingdao Agricultural University, Qingdao, Shandong 266109, China e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

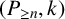A graph G is called a $(P_{\geq n},k)$ -factor-critical covered graph if for any 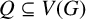$Q\subseteq V(G)$ with 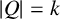$|Q|=k$ and any 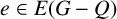$e\in E(G-Q)$ , 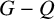$G-Q$ has a 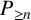$P_{\geq n}$ -factor covering e. We demonstrate that (i) a 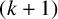$(k+1)$ -connected graph G with at least 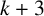$k+3$ vertices is a 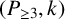$(P_{\geq 3},k)$ -factor-critical covered graph if its toughness 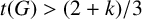$t(G)>{(2+k)}/{3}$ ; (ii) a 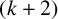$(k+2)$ -connected graph G is a 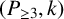$(P_{\geq 3},k)$ -factor-critical covered graph if its isolated toughness 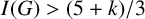$I(G)>{(5+k)}/{3}$ . Furthermore, we show that the conditions on 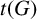$t(G)$ and 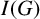$I(G)$ are sharp.

Keywords

graphtoughnessisolated toughnessP≥3-factor(P≥3, k)-factor-critical covered graph

MSC classification

Primary: 05C70: Factorization, matching, partitioning, covering and packing
Secondary: 05C38: Paths and cycles
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 106 , Issue 2 , October 2022 , pp. 195 - 202
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work is supported by the Six Talent Peaks Project in Jiangsu Province, China (Grant No. JY–022).

References

Chvátal, V., ‘Tough graphs and Hamiltonian circuits’, Discrete Math. 5 (1973), 215–228.CrossRefGoogle Scholar
Enomoto, H., Jackson, B., Katerinis, P. and Satio, A., ‘Toughness and the existence of $k$ -factors’, J. Graph Theory 9 (1985), 87–95.CrossRefGoogle Scholar
Gao, W., Guirao, J. and Chen, Y., ‘A toughness condition for fractional $\left(k,m\right)$ -deleted graphs revisited’, Acta Math. Sin. (Engl. Ser.) 35 (2019), 1227–1237.CrossRefGoogle Scholar
Gao, W., Liang, L. and Chen, Y., ‘An isolated toughness condition for graphs to be fractional $\left(k,m\right)$ -deleted graphs’, Util. Math. 105 (2017), 303–316.Google Scholar
Gao, W. and Wang, W., ‘New isolated toughness condition for fractional $\left(g,f,n\right)$ -critical graphs’, Colloq. Math. 147 (2017), 55–65.CrossRefGoogle Scholar
Gao, W., Wang, W. and Dimitrov, D., ‘Toughness condition for a graph to be all fractional $\left(g,f,n\right)$ -critical deleted’, Filomat 33(9) (2019), 2735–2746.CrossRefGoogle Scholar
Johnson, M., Paulusma, D. and Wood, C., ‘Path factors and parallel knock-out schemes of almost claw-free graphs’, Discrete Math. 310 (2010), 1413–1423.CrossRefGoogle Scholar
Kaneko, A., ‘A necessary and sufficient condition for the existence of a path factor every component of which is a path of length at least two’, J. Combin. Theory Ser. B 88 (2003), 195–218.CrossRefGoogle Scholar
Kano, M., Katona, G. Y. and Király, Z., ‘Packing paths of length at least two’, Discrete Math. 283 (2004), 129–135.CrossRefGoogle Scholar
Katerinis, P., ‘Toughness of graphs and the existence of factors’, Discrete Math. 80 (1990), 81–92.CrossRefGoogle Scholar
Kelmans, A., ‘Packing 3-vertex paths in claw-free graphs and related topics’, Discrete Appl. Math. 159 (2011), 112–127.CrossRefGoogle Scholar
Liu, G. and Zhang, L., ‘Toughness and the existence of fractional $k$ -factors of graphs’, Discrete Math. 308 (2008), 1741–1748.CrossRefGoogle Scholar
Yang, J., Ma, Y. and Liu, G., ‘Fractional $\left(g,f\right)$ -factors in graphs’, Appl. Math. J. Chinese Univ. Ser. A 16 (2001), 385–390.Google Scholar
Zhang, H. and Zhou, S., ‘Characterizations for ${P}_{\ge 2}$ -factor and ${P}_{\ge 3}$ -factor covered graphs’, Discrete Math. 309 (2009), 2067–2076.CrossRefGoogle Scholar
Zhou, S., ‘Some results about component factors in graphs’, RAIRO Oper. Res. 53(3) (2019), 723–730.CrossRefGoogle Scholar
Zhou, S., ‘Remarks on path factors in graphs’, RAIRO Oper. Res. 54(6) (2020), 1827–1834.CrossRefGoogle Scholar
Zhou, S., Bian, Q. and Pan, Q., ‘Path factors in subgraphs’, Discrete Appl. Math., to appear; doi:10.1016/j.dam.2021.04.012.CrossRefGoogle Scholar
Zhou, S., Pan, Q. and Xu, L., ‘Isolated toughness for fractional $\left(2,b,k\right)$ -critical covered graphs’, Preprint.Google Scholar
Zhou, S., Sun, Z. and Liu, H., ‘Isolated toughness and path-factor uniform graphs’, RAIRO Oper. Res. 55(3) (2021), 1279–1290.CrossRefGoogle Scholar
Zhou, S., Sun, Z. and Liu, H., ‘On ${P}_{\ge 3}$ -factor deleted graphs’, Acta Math. Appl. Sin. Engl. Ser., to appear.Google Scholar
Zhou, S., Wu, J. and Zhang, T., ‘The existence of ${P}_{\ge 3}$ -factor covered graphs’, Discuss. Math. Graph Theory 37(4) (2017), 1055–1065.Google Scholar
Zhou, S., Xu, J. and Xu, L., ‘Component factors and binding number conditions in graphs’, AIMS Math. 6(11) (2021), 12460–12470.CrossRefGoogle Scholar