Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-24T18:40:20.131Z Has data issue: false hasContentIssue false
  • English
  • Français

THE TOTAL DISTANCE FOR TOTALLY POSITIVE ALGEBRAIC INTEGERS

Part of: Algebraic number theory: global fields

Published online by Cambridge University Press:  09 September 2014

V. FLAMMANG
V. FLAMMANG*
Affiliation:
UMR CNRS 7502, IECL, Université de Lorraine, site de Metz, Département de Mathématiques, UFR MIM, Ile du Saulcy, CS 50128. 57045 METZ cedex 01, France email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 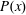$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}P(x)$ be a polynomial of degree 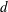$d$ with zeros 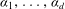$\alpha _1, \ldots, \alpha _d$. Stulov and Yang [‘An elementary inequality about the Mahler measure’, Involve6(4) (2013), 393–397] defined the total distance of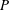$P$ as 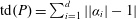${\rm td}(P)=\sum _{i=1}^{d} | | \alpha _i| -1|$. In this paper, using the method of explicit auxiliary functions, we study the spectrum of the total distance for totally positive algebraic integers and find its five smallest points. Moreover, for totally positive algebraic integers, we establish inequalities comparing the total distance with two standard measures and also the trace. We give numerical examples to show that our bounds are quite good. The polynomials involved in the auxiliary functions are found by a recursive algorithm.

Keywords

totally positive algebraic integerstotal distanceMahler measureexplicit auxiliary functions

MSC classification

Secondary: 11R06: PV-numbers and generalizations; other special algebraic numbers; Mahler measure
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 90 , Issue 3 , December 2014 , pp. 391 - 403
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Aguirre, J., Bilbao, M. and Peral, J. C., ‘The trace of totally positive algebraic integers’, Math. Comp. 75(253) (2006), 385–393.CrossRefGoogle Scholar
Amoroso, F., ‘f-transfinite diameter and number theoretic applications’, Ann. Inst. Fourier (Grenoble) 43 (1993), 1179–1198.CrossRefGoogle Scholar
Flammang, V., ‘On the absolute trace of polynomials having all zeros in a sector’, Experiment. Math. 17(4) (2008), 443–450.Google Scholar
Flammang, V., ‘Trace of totally positive algebraic integers and integer transfinite diameter’, Math. Comp. 78(266) (2009), 1119–1125.CrossRefGoogle Scholar
Flammang, V., ‘Comparison of measures of totally positive polynomials’, Bull. Aust. Math. Soc. 89(2) (2014), 265–270.CrossRefGoogle Scholar
Flammang, V. and Rhin, G., ‘On the absolute Mahler measure of polynomials having all zeros in a sector III’, Math. Comp., to appear.Google Scholar
Flammang, V., ‘Construction de fonctions auxiliaires. Application aux mesures de certaines familles d’entiers algébriques’, to appear.Google Scholar
Kronecker, L., ‘Zwei Sätze über Gleichugen mit ganzzahligen Koeffizienten’, J. reine angew. Math. 53 (1857), 173–175.Google Scholar
Langevin, M., ‘Minorations de la maison et de la mesure de Mahler de certains entiers algébriques’, C. R. Acad. Sci. Paris 303 (1986), 523–526.Google Scholar
Rhin, G. and Smyth, C. J., ‘On the absolute Mahler measure of polynomials having all zeros in a sector’, Math. Comp. 64(209) (1995), 295–304.CrossRefGoogle Scholar
Rhin, G. and Wu, Q., ‘On the absolute Mahler measure of polynomials having all zeros in a sector II’, Math. Comp. 74(249) (2004), 383–388.Google Scholar
Schur, I., ‘Über die Verteilung der Wurzeln bei gewissen algebraischen Gleichungen mit ganzzahligen Koeffizienten’, Math. Z. 1 (1918), 377–402.CrossRefGoogle Scholar
Siegel, C. L., ‘The trace of totally positive and real algebraic integers’, Ann. of Math. (2) 46 (1945), 302–312.CrossRefGoogle Scholar
Smyth, C. J., ‘The mean value of totally real algebraic numbers’, Math. Comp. 42 (1984), 663–681.Google Scholar
Stulov, K. and Yang, R., ‘An elementary inequality about the Mahler measure’, Involve 6(4) (2013), 393–397.CrossRefGoogle Scholar
Wu, Q., ‘On the linear independence measure of logarithms of rational numbers’, Math. Comp. 72 (2003), 901–911.CrossRefGoogle Scholar
Wu, Q. and Wang, L., ‘On the irrationality measure of log 3’, J. Number Theory 142 (2014), 264–273.CrossRefGoogle Scholar