Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-28T00:17:53.651Z Has data issue: false hasContentIssue false
  • English
  • Français

A TORSION-FREE ABELIAN GROUP EXISTS WHOSE QUOTIENT GROUP MODULO THE SQUARE SUBGROUP IS NOT A NIL-GROUP

Part of: Abelian groups General commutative ring theory

Published online by Cambridge University Press:  30 August 2016

R. R. ANDRUSZKIEWICZ  and
M. WORONOWICZ
R. R. ANDRUSZKIEWICZ*
Affiliation:
Institute of Mathematics, University of Białystok, 15-267 Białystok, K. Ciołkowskiego 1M, Poland email [email protected]
M. WORONOWICZ
Affiliation:
Institute of Mathematics, University of Białystok, 15-267 Białystok, K. Ciołkowskiego 1M, Poland email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The first example of a torsion-free abelian group 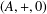$(A,+,0)$ such that the quotient group of 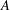$A$ modulo the square subgroup is not a nil-group is indicated (for both associative and general rings). In particular, the answer to the question posed by Stratton and Webb [‘Abelian groups, nil modulo a subgroup, need not have nil quotient group’, Publ. Math. Debrecen27 (1980), 127–130] is given for torsion-free groups. A new method of constructing indecomposable nil-groups of any rank from 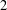$2$ to 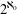$2^{\aleph _{0}}$ is presented. Ring multiplications on 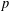$p$-pure subgroups of the additive group of the ring of 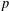$p$-adic integers are investigated using only elementary methods.

Keywords

nil-groupssquare subgroupsabelian groups

MSC classification

Primary: 20K99: None of the above, but in this section
Secondary: 13A99: None of the above, but in this section
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 94 , Issue 3 , December 2016 , pp. 449 - 456
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Aghdam, A. M., ‘Square subgroup of an Abelian group’, Acta. Sci. Math. 51 (1987), 343–348.Google Scholar
Aghdam, A. M. and Najafizadeh, A., ‘Square subgroups of rank two Abelian groups’, Colloq. Math. 117(1) (2009), 19–28.CrossRefGoogle Scholar
Aghdam, A. M. and Najafizadeh, A., ‘Square submodule of a module’, Mediterr. J. Math. 7(2) (2010), 195–207.CrossRefGoogle Scholar
Aghdam, A. M. and Najafizadeh, A., ‘On the indecomposable torsion-free abelian groups of rank two’, Rocky Mountain J. Math. 42(2) (2012), 425–438.Google Scholar
Andruszkiewicz, R. R. and Woronowicz, M., ‘On SI -groups’, Bull. Aust. Math. Soc. 91 (2015), 92–103.CrossRefGoogle Scholar
Andruszkiewicz, R. R. and Woronowicz, M., ‘Some new results for the square subgroup of an abelian group’, Comm. Algebra 44(6) (2016), 2351–2361.CrossRefGoogle Scholar
Borevich, Z. I. and Shafarevich, I. R., Number Theory (Academic Press, New York–San Francisco–London, 1966).Google Scholar
Feigelstock, S., Additive groups of rings, Vol. 1 (Pitman Advanced Publishing Program, Boston, 1983).Google Scholar
Feigelstock, S., ‘Additive groups self-injective rings’, Soochow J. Math. 33(4) (2007), 641–645.Google Scholar
Fuchs, L., Abelian Groups (Akadémiai Kiadó, Budapest, 1966).Google Scholar
Fuchs, L., Infinite Abelian Groups, Vol. 1 (Academic Press, New York–London, 1970).Google Scholar
Fuchs, L., Infinite Abelian Groups, Vol. 2 (Academic Press, New York–London, 1973).Google Scholar
Kompantseva, E. I., ‘Absolute nil-ideals of Abelian groups’, Fundam. Prikl. Mat. 17(8) (2012), 63–76.Google Scholar
Kompantseva, E. I., ‘Abelian dqt-groups and rings on them’, Fundam. Prikl. Mat. 18(3) (2013), 53–67.Google Scholar
Najafizadeh, A., ‘On the square submodule of a mixed module’, Gen. Math. Notes 27(1) (2015), 1–8.Google Scholar
Stratton, A. E. and Webb, M. C., ‘Abelian groups, nil modulo a subgroup, need not have nil quotient group’, Publ. Math. Debrecen 27 (1980), 127–130.Google Scholar
Thi Thu Thuy, Pham, ‘Torsion Abelian RAI-Groups’, J. Math. Sci. (N. Y.) 197(5) (2014), 658–678.Google Scholar
Thi Thu Thuy, Pham, ‘Torsion Abelian afi-Groups’, J. Math. Sci. (N. Y.) 197(5) (2014), 679–683.Google Scholar