Article contents
Torsion in the additive group of relatively free Lie rings
Published online by Cambridge University Press: 17 April 2009
Abstract
Let L = L(X) be the free Lie ring of countable rank and let p be prime. Then L(Vp) = L/[(L')p, L] is the relatively free ring for the variety of Lie rings Vp = [Np−1A, E] and Vp is defined by the identity
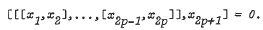
The purpose of this note is to establish that there exist elements of order p in the additive group of L(Vp). Previously, the existence of p-torsion was proved by Kuz'min for p = 2 only. Similar results were obtained for varieties of groups by Gupta when p = 2 and by Stöhr when p = 3.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1986
References
- 2
- Cited by


