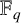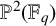TANGENT-FILLING PLANE CURVES OVER FINITE FIELDS

Abstract

We study plane curves over finite fields whose tangent lines at smooth $\mathbb {F}_q$-points together cover all the points of $\mathbb {P}^2(\mathbb {F}_q)$.

1 Introduction

The investigation of algebraic curves over finite fields is an ever-growing research topic. Stemming from the intersection of algebra, number theory and algebraic geometry, it influences a wide array of fields such as coding theory and combinatorial design theory [19]. As one specific example in this vast body of work, finding curves with many $\mathbb {F}_q$ -rational points remains an interesting challenge. The motivation behind searching for extremal curves ranges from purely theoretical reasons (for example, understanding the sharpness of the Hasse–Weil inequality) to more applied constructions (for example, obtaining a rich configuration of points).

It is already instructive to restrict attention to plane curves. We list a few different definitions from the literature for a given projective irreducible plane curve $C\subset \mathbb {P}^2$ of degree d over a finite field $\mathbb {F}_q$ to have ‘many $\mathbb {F}_q$ -rational points’.

1. (a) We say that C is a maximal curve if $\#C(\mathbb {F}_q) = q+1 + (d-1)(d-2)\sqrt {q}$ , that is, the curve achieves the Hasse–Weil upper bound for its $\mathbb {F}_q$ -rational points.

2. (b) We say that C is plane-filling if $C(\mathbb {F}_q)=\mathbb {P}^2(\mathbb {F}_q)$ , that is, C contains each of the $q^2+q+1$ distinct $\mathbb {F}_q$ -points of $\mathbb {P}^2$ .

3. (c) We say that C is blocking if $C(\mathbb {F}_q)$ is a blocking set, that is, C meets every $\mathbb {F}_q$ -line L at some $\mathbb {F}_q$ -point.

The main purpose of the present paper is to introduce a new concept that indicates in yet another way that the curve contains many $\mathbb {F}_q$ -points.

1. (d) We say that C is tangent-filling if every point $P\in \mathbb {P}^2(\mathbb {F}_q)$ lies on a tangent line $T_Q C$ to the curve C at some smooth $\mathbb {F}_q$ -point Q.

Regarding the literature, we note that curves satisfying (a) have been thoroughly studied in many papers ranging from foundational work [13, 15, 16] to more recent discoveries [9, 10]. Curves satisfying (b) have been analysed in [14, 20, 21]. Finally, curves satisfying (c) have been examined by the authors in joint work with Yip [2–5].

Our first theorem shows that a curve of low degree cannot be tangent-filling. We first state the result when the ground field is $\mathbb {F}_p$ for some prime p. For convenience, we state the result for $d\geq 3$ and discuss the case $d=2$ in Remark 2.2.

Theorem 1.1. Let $C\subset \mathbb {P}^2$ be an irreducible plane curve of degree $d\geq 3$ defined over $\mathbb {F}_p$ , where p is a prime. If $p\geq 4(d-1)^2(d-2)^2$ , then C is not tangent-filling.

We have an analogous result for an arbitrary finite field $\mathbb {F}_q$ .

Theorem 1.2. Let $C\subset \mathbb {P}^2$ be an irreducible plane curve of degree $d\geq 2$ defined over $\mathbb {F}_q$ . If $p>d$ and $q\geq d^2(d-1)^6$ , then C is not tangent-filling.

Let us briefly compare the bounds in these two theorems. The bound $p\geq O(d^4)$ in Theorem 1.1 is replaced by a pair of bounds $p>d$ and $q\geq O(d^8)$ in Theorem 1.2. From one perspective, Theorem 1.2 provides worse bounds on q, and it remains open to improve $q\geq O(d^8)$ to $q\geq O(d^4)$ . From another perspective, Theorem 1.2 provides better bounds on the characteristic p; for instance, when $q=p^n$ with $n=4$ , the bound $p^4=q\geq O(d^8)$ is equivalent to $p\geq O(d^2)$ , which is a weaker hypothesis than the earlier bound $p\geq O(d^4)$ . It is also natural to consider the situation where we confine our attention to a more restrictive class of smooth curves; Remark 2.3 explains such a slightly improved result.

We are also interested in finding examples of tangent-filling curves. Clearly, any smooth plane-filling curve is tangent-filling. Since the minimum degree of a smooth plane-filling curve over $\mathbb {F}_q$ is $q+2$ by [21], it is natural to search for tangent-filling curves with degrees less than $q+2$ . Our next theorem exhibits an example of a tangent-filling curve of degree $q-1$ .

Theorem 1.3. Let $q\geq 11$ and $p=\operatorname {char}(\mathbb {F}_q)>3$ . The curve C defined by the equation

$$ \begin{align*} x^{q-1} + y^{q-1} + z^{q-1} - 3(x+y+z)^{q-1} = 0 \end{align*} $$

is an irreducible tangent-filling curve.

Remark 1.4. If $\mathrm {char}(\mathbb {F}_q)=2$ in Theorem 1.3, then the curve C is reducible, as it contains the lines $x=y$ , $y=z$ and $z=x$ .

If $\mathrm {char}(\mathbb {F}_q)=3$ , then the curve C in Theorem 1.3 is smooth, but it is not tangent-filling since no tangent line at a point of $C(\mathbb {F}_q)$ passes through any of the points $[1:0:0]$ , $[0:1:0]$ and $[0:0:1]$ . This claim can be easily checked since the points $[x_0:y_0:z_0]\in C(\mathbb {F}_q)$ have the property that $x_0y_0z_0\ne 0$ (the proof of this fact follows as in Lemma 3.2, which characterises the $\mathbb {F}_q$ -points of C when $\mathrm {char}(\mathbb {F}_q)>3$ ), while the equation of the tangent line at the point $[x_0:y_0:z_0]\in C(\mathbb {F}_q)$ is

$$ \begin{align*}x_0^{q-2}\cdot x + y_0^{q-2}\cdot y + z_0^{q-2}\cdot z = 0.\end{align*} $$

Finally, a simple computer check shows that the curve C from Theorem 1.3 is not tangent-filling when $q\in \{5,7\}$ (see also Remark 3.7).

While we expect that $d=q-1$ is not the smallest possible degree of a tangent-filling curve, we believe that Theorem 1.3 is novel in several ways. First, checking the tangent-filling condition over $\mathbb {F}_q$ requires careful analysis of the $\mathbb {F}_q$ -points of the curve. Second, in our previous work with Yip [2], we found several families of blocking smooth curves of degree less than q, and so it was natural to test whether those families are also tangent-filling; however, none of the families of blocking smooth curves tested turned out to be tangent-filling. This suggests that finding tangent-filling curves may be very challenging, much more so than the case of blocking curves. In particular, finding tangent-filling curves of degree less than q seems very difficult in general. Quite interestingly, the curve from Theorem 1.3 is not blocking since $C(\mathbb {F}_q)$ does not intersect the $\mathbb {F}_q$ -lines $x=0$ , $y=0$ , $z=0$ and $x+y+z=0$ (see also Corollary 3.3).

We remark that when q has a special form, there are more optimal examples. The noteworthy example is the Hermitian curve $\mathcal {H}_q$ defined by $x^{\sqrt {q}+1} + y^{\sqrt {q}+1} + z^{\sqrt {q}+1} = 0$ when q is a square. We will see in Example 3.1 that $\mathcal {H}_q$ is a tangent-filling curve. Thus, for q square, there is a (smooth) tangent-filling curve of degree $\sqrt {q}+1$ .

Inspired by the example in the previous paragraph, we may ask for the most optimal curve that has the tangent-filling property.

Question 1.5. What is the minimum degree of an irreducible tangent-filling plane curve over $\mathbb {F}_q$ ?

Let us explain a heuristic that suggests that the optimal degree may not be too far away from $\sqrt {q}$ even for a general q. Consider a collection $\mathcal {L}$ of $\mathbb {F}_q$ -lines such that

(1.1) $$ \begin{align} \bigcup_{L\in \mathcal{L}} L(\mathbb{F}_q) = \mathbb{P}^2(\mathbb{F}_q). \end{align} $$

By viewing each line as a point in the dual space $(\mathbb {P}^2)^{\ast }$ , the condition (1.1) is equivalent to $\mathcal {L}$ being a blocking set in $(\mathbb {P}^2)^{\ast }(\mathbb {F}_q)$ . There are plenty of blocking sets with size a constant multiple of q; for instance, the so-called projective triangle, a well-known example of a blocking set, has $\tfrac 32(q+1)$ points for odd q [18]. So, we choose $\mathcal {L}$ satisfying (1.1) and $|\mathcal {L}|=c_0 q$ for some constant $c_0>0$ . Next, suppose that it is possible to pick distinct $\mathbb {F}_q$ -points $P_i\in L_i$ for each $L_i\in \mathcal {L}$ , so that $P_i\neq P_j$ for $i\neq j$ . Let us impose the condition that a curve of degree d passes through the point $P_i$ and has contact order at least $2$ with the line $L_i$ at the point $P_i$ . For each value of i, this imposes two linear conditions in the parameter space $\mathbb {P}^N$ of plane curves of degree d, where $N=\binom {d+2}{2}-1$ . Assuming that $\binom {d+2}{2}-1> 2 |\mathcal {L}| = 2c_0q$ , we obtain a curve of degree d satisfying each of these local conditions. By construction, each such curve is tangent to the line $L_i$ at the point $P_i$ and the tangent-filling property is enforced by (1.1). The main issue is that all such resulting curves may be singular at one (or more) of the points $P_i$ . While the bound of the form $d> c_1\sqrt {q}$ for some constant $c_1>0$ is predicted by this heuristic, it seems very challenging to make this interpolation argument precise.

Structure of the paper

In Section 2 we borrow tools from classical algebraic geometry and combinatorics of blocking sets to prove Theorems 1.1 and 1.2. In Section 3 we prove Theorem 1.3 by studying in detail the geometric properties of the given curve C, such as its singular locus and irreducibility, along with an arithmetic analysis for the equation of a tangent line at a smooth $\mathbb {F}_q$ -point of C.

2 Curves of low degree are not tangent-filling

We start with preliminary geometric constructions. Given a plane curve C, recall that the dual curve $C^{\ast }$ parametrises the tangent lines to C. More formally, $C^{\ast }$ is the closure of the image of the Gauss map $\gamma _G\colon C\to (\mathbb {P}^{2})^{\ast }$ mapping a regular point P on C to the line $T_P C$ .

When the Gauss map $\gamma _G$ is separable, the geometry of the tangent lines to the curve in characteristic p is similar to the behaviour observed in characteristic $0$ . It turns out that the curve C is reflexive (that is, the double dual $(C^{\ast })^{\ast }$ can be canonically identified with C itself) if and only if $\gamma _G$ is separable [25]. Thus, all curves in characteristic $0$ are reflexive. In positive characteristic p, the condition $p>d$ is sufficient to ensure that a plane curve of degree d is reflexive [23, Proposition 1.5].

2.1 Bitangents

For a given plane curve C, we say that a line L is bitangent to C if L is tangent to the curve C at two or more points. The following is a well-known result in classical algebraic geometry; we include its proof to emphasise how the hypothesis $p>d$ is used. Since it is possible to have a curve with infinitely many bitangents [24, Example 2], the lemma below would not be true if we completely removed the assumption $p>d$ .

Lemma 2.1. Let $C\subset \mathbb {P}^2$ be a geometrically irreducible plane curve of degree $d\geq 2$ defined over $\mathbb {F}_q$ such that $p>d$ . Then C has at most $ \tfrac 12d^2(d-1)^2$ bitangents.

Proof. The condition $p>d$ guarantees that the Gauss map $\gamma _G$ is separable. The dual curve $C^{\ast }$ has degree $\delta \leq d(d-1)$ . Since $C^{\ast }$ is geometrically irreducible, it has at most $\binom {\delta -1}{2}$ singular points [17, Exercise 20.18]. Every bitangent of the curve C corresponds to some singular point of $C^{\ast }$ because $\gamma _G$ is separable [25]. Thus, the number of bitangents to C is at most

$$ \begin{align*} \binom{\delta-1}{2} \leq \binom{d(d-1)-1}{2} = \frac{1}{2}(d^2-d-1)(d^2-d-2) \leq \frac{1}{2}(d^2-d)(d^2-d).\\[-44pt] \end{align*} $$

The previous lemma would hold if we replaced the hypothesis $p>d$ with the weaker hypothesis that the Gauss map of C is separable.

2.2 Strange curves

We say that an irreducible plane curve C of degree $d\geq 2$ over a field K is strange if all the tangent lines to the curve C at its smooth $\overline {K}$ -points are concurrent. This is equivalent to requiring that the dual curve of C is a line. Since the double dual of a strange curve cannot be the original curve, it follows that strange curves must be nonreflexive. In particular, strange curves can only exist when ${p=\operatorname {char}(K)>0}$ . Strange curves do exist [24, Example 1]: for instance, all the tangent lines to the curve $xy^{p-1}-z^p=0$ pass through the point $[0:0:1]$ . The paper [8] contains several results on various properties and characterisations of strange curves.

As mentioned at the beginning of the section, the hypothesis $p>d$ ensures that the curve is reflexive. Thus, a plane curve of degree $d\geq 2$ cannot be strange whenever $p>d$ . This fact will be crucial in the proofs below, when we verify that the $\mathbb {F}_q$ -points of the dual curve $C^{\ast }$ do not produce a trivial blocking set.

2.3 Proofs of Theorems 1.1 and 1.2

We now present the proof of our first main theorem which roughly states that tangent-filling curves over $\mathbb {F}_p$ cannot exist when p is larger than a quartic function of d.

Proof of Theorem 1.1.

We first assume that C is geometrically irreducible. We start by observing that the hypothesis $p\geq 4(d-1)^2(d-2)^2$ implies $p>d$ for $d\geq 3$ . Thus, the curve C is reflexive, and, in particular, C is not strange, meaning that $\deg (C^{\ast })>1$ . By applying the Hasse–Weil bound [6, Corollary 2.5], we have

$$ \begin{align*} \# C(\mathbb{F}_p) \leq p+1 + (d-1)(d-2) \sqrt{p}. \end{align*} $$

Suppose, to the contrary, that C is tangent-filling. Let $B\subseteq C^{\ast }(\mathbb {F}_q)$ correspond to the set of tangent $\mathbb {F}_p$ -lines to the curve C at smooth $\mathbb {F}_p$ -points. It is clear that

(2.1) $$ \begin{align} \# B \leq \# C(\mathbb{F}_p)\leq p+1 + (d-1)(d-2) \sqrt{p}. \end{align} $$

Note that B is a blocking set by definition of tangent-filling; indeed, each $\mathbb {F}_p$ -line in the dual projective plane parametrises lines passing through a fixed point, so B meets every $\mathbb {F}_p$ -line in the dual space. Since $1<\deg (C^{\ast })\leq d(d-1) < p+1$ , the set B is a nontrivial blocking set, that is, B cannot contain all the $\mathbb {F}_p$ -points of some $\mathbb {F}_p$ -line in $(\mathbb {P}^2)^{\ast }(\mathbb {F}_p)$ . Indeed, $C^{\ast }$ is irreducible (as it is the image of the irreducible curve C through the map $\gamma _G$ ) and has degree less than $p+1$ . By Blokhuis’s theorem [11],

(2.2) $$ \begin{align} \#B\geq \tfrac{3}{2}(p+1). \end{align} $$

Combining (2.1) and (2.2), we get $p+1 + (d-1)(d-2) \sqrt {p} \geq \tfrac 32(p+1)$ which contradicts the hypothesis $p\geq 4(d-1)^2(d-2)^2$ .

Now, suppose that C is not geometrically irreducible. Since C is irreducible but not geometrically irreducible, we conclude that $\# C(\mathbb {F}_p) \leq \tfrac 14d^2$ (see [12, Lemma 2.3] or [1, Remark 2.2]). In particular, the number of distinct $\mathbb {F}_p$ -tangent lines to C is at most $\tfrac 14d^2$ . Since each $\mathbb {F}_p$ -line covers $p+1$ points of $\mathbb {P}^2(\mathbb {F}_p)$ , all the tangent lines to C at its smooth $\mathbb {F}_p$ -points together can cover at most $\tfrac 14 d^2\cdot (p+1)$ distinct $\mathbb {F}_q$ -points. Since $p\geq 4(d-1)^2(d-2)^2$ , it is immediate that $\tfrac 14d^2\cdot (p+1)<p^2+p+1$ , so C is not tangent-filling.

Remark 2.2. The inequality $p\geq 4(d-1)^2(d-2)^2$ automatically implies $p>d$ when $d\geq 3$ . However, when $d=2$ , the inequality $p\geq 4(d-1)^2(d-2)^2$ is vacuous and $p=2$ is allowed. When $p=2$ and $d=2$ , the smooth conics are strange curves, which are therefore tangent-filling because the tangent lines at the $\mathbb {F}_q$ -rational points of this conic are all the $q+1$ lines passing through some given point in $\mathbb {P}^2(\mathbb {F}_q)$ . So, Theorem 1.1 does not hold when $p=d=2$ ; on the other hand, Theorem 1.1 continues to hold when $d=2$ and $p>2$ with essentially the same proof as the one above.

Proof of Theorem 1.2.

We first assume that the curve C is geometrically irreducible, that is, irreducible over $\overline {\mathbb {F}_q}$ . We claim that $C^{\ast }$ is not a blocking curve. Suppose, to the contrary, that $C^{\ast }(\mathbb {F}_q)$ is a blocking set in $(\mathbb {P}^2)^{\ast }(\mathbb {F}_q)$ . Since $p>d$ , the curve C is not strange, that is, $\deg (C^{\ast })>1$ . Since $1<\deg (C^{\ast })\leq d(d-1) < q+1$ , the set B is a nontrivial blocking set by the reasoning given in the proof of Theorem 1.1. By [4, Lemma 4.1],

(2.3) $$ \begin{align} \# C^{\ast}(\mathbb{F}_q)> q + \frac{q+\sqrt{q}}{\deg(C^{\ast})} \geq q + \frac{q+\sqrt{q}}{d(d-1)}. \end{align} $$

On the other hand, the number of $\mathbb {F}_q$ -points on the dual curve $C^{\ast }$ is bounded above:

(2.4) $$ \begin{align} \# C^{\ast}(\mathbb{F}_q)\leq \#C(\mathbb{F}_q) + \# \{\text{bitangents to } C \text{ defined over } \mathbb{F}_q\}. \end{align} $$

Combining Lemma 2.1, the Hasse–Weil bound applied to C [6, Corollary 2.5], and (2.4), we obtain an upper bound:

(2.5) $$ \begin{align} \# C^{\ast}(\mathbb{F}_q)\leq q+1 + (d-1)(d-2)\sqrt{q} + \tfrac{1}{2} d^2(d-1)^2. \end{align} $$

Comparing (2.3) and (2.5),

$$ \begin{align*} (d-1)(d-2)\sqrt{q} + \frac{1}{2} d^2(d-1)^2 + 1> \frac{q+\sqrt{q}}{d(d-1)}, \end{align*} $$

or equivalently,

(2.6) $$ \begin{align} d(d-1)^2(d-2)\sqrt{q} + \tfrac{1}{2}d^3(d-1)^3 + d(d-1)> q + \sqrt{q}. \end{align} $$

Since $\sqrt {q}\geq d(d-1)^3$ , we have $\sqrt {q}\geq \tfrac 12 d^2(d-1)$ which allows us to deduce that

$$ \begin{align*} q + \sqrt{q} &\geq d(d-1)^2 \cdot ((d-1)\sqrt{q}) + \sqrt{q} \\ &\geq d(d-1)^2 \cdot ((d-2)\sqrt{q}+\sqrt{q}) + d(d-1) \\ &\geq d(d-1)^2 \cdot ((d-2)\sqrt{q} + \tfrac{1}{2}d^2(d-1)) + d(d-1) \\ &=d(d-1)^2 (d-2)\sqrt{q} + \tfrac{1}{2}d^3(d-1)^3 + d(d-1), \end{align*} $$

contradicting (2.6). We conclude that $C^{\ast }$ is not a blocking curve, which means that C is not tangent-filling.

When C is irreducible but not geometrically irreducible, $\# C(\mathbb {F}_q)\leq \tfrac 14d^2$ , so we apply the argument (with p replaced by q everywhere) from the end of the proof of Theorem 1.1. We conclude that C is still not tangent-filling.

Remark 2.3. Kaji [22] proved that the Gauss map of a smooth plane curve over $\overline {\mathbb {F}_q}$ must be purely inseparable. Consequently, a smooth plane curve must have finitely many bitagents. Moreover, only smooth strange curves are conics in characteristic $2$ . These observations together tell us that Theorem 1.2 holds for smooth curves even when the hypothesis $p\geq d$ is removed as long as $d\geq 3$ .

3 Explicit examples of tangent-filling curves

We start with an example of a plane curve of degree $\sqrt {q}+1$ which is tangent-filling over $\mathbb {F}_q$ when q is a square.

Example 3.1. Let q be a prime power such that q is a square. The curve $\mathcal {H}_q$ defined by

$$ \begin{align*} x^{\sqrt{q}+1} + y^{\sqrt{q}+1} + z^{\sqrt{q}+1} = 0 \end{align*} $$

is tangent-filling over $\mathbb {F}_q$ . The curve $\mathcal {H}_q$ is known as the Hermitian curve in the literature. It can be checked that $\mathcal {H}_q$ has exactly $(\sqrt {q})^3+1$ distinct $\mathbb {F}_q$ -points. Moreover, the set $\mathcal {H}_q(\mathbb {F}_q)$ forms a unital in the sense of combinatorial geometry, meaning that the points can be arranged into subsets of size $\sqrt {q}+1$ so that any two points of $\mathcal {H}_q(\mathbb {F}_q)$ lie in a unique subset. In particular, it can be shown that every $\mathbb {F}_q$ -line meets $\mathcal {H}_q(\mathbb {F}_q)$ at either $1$ or $\sqrt {q}+1$ points [7, Theorem 2.2]. As a result, $\mathcal {H}_q$ is a blocking curve over $\mathbb {F}_q$ .

To show that $\mathcal {H}_q$ is a tangent-filling curve, we let $P_0=[a:b:c]$ be a point in $\mathbb {P}^2(\mathbb {F}_q)$ . We are searching for a point $Q=[x_0:y_0:z_0]\in \mathcal {H}_q(\mathbb {F}_q)$ such that $T_Q(C)$ contains $P_0$ . This is equivalent to finding $[x_0:y_0:z_0]\in \mathcal {H}_q(\mathbb {F}_q)$ such that

$$ \begin{align*} x_0^{ \sqrt{q}} a + y_0^{\sqrt{q}} b + z_0^{\sqrt{q}} c = 0. \end{align*} $$

We remark that the map $[x:y:z]\mapsto [x^{\sqrt {q}}:y^{\sqrt {q}}:z^{\sqrt {q}}]$ is a bijection on the set $\mathbb {P}^2(\mathbb {F}_q)$ , and therefore also on $\mathcal {H}_q(\mathbb {F}_q)$ because $\mathcal {H}_q(\mathbb {F}_q)$ is defined over $\mathbb {F}_q$ . Thus, there exists ${[x_1:y_1:z_1]\in \mathcal {H}_q(\mathbb {F}_q)}$ with the property that

$$ \begin{align*}[x_0:y_0:z_0]=[x_1^{\sqrt{q}}:y_1^{\sqrt{q}}:z_1^{\sqrt{q}}].\end{align*} $$

In other words, it suffices to find $[x_1:y_1:z_1]\in \mathcal {H}_q(\mathbb {F}_q)$ such that

(3.1) $$ \begin{align} x_1^{q} a + y_1^{q} b + z_1^{q} c = 0. \end{align} $$

Since $x_1, y_1, z_1$ are elements of $\mathbb {F}_q$ , we see that (3.1) is equivalent to

(3.2) $$ \begin{align} x_1 a + y_1 b + z_1 c = 0. \end{align} $$

Let L be the $\mathbb {F}_q$ -line defined by $ax+by+cz=0$ . Since $\mathcal {H}_q(\mathbb {F}_q)$ is a blocking set, Equation (3.2) is satisfied for some $Q=[x_1:y_1:z_1]\in \mathcal {H}_q(\mathbb {F}_q)$ , as claimed. This argument also shows that the dual of the Hermitian curve is isomorphic to itself.

For the remainder of the paper, we will focus on the curve C defined by the equation

(3.3) $$ \begin{align} x^{q-1} + y^{q-1} + z^{q-1} - 3(x+y+z)^{q-1} = 0. \end{align} $$

Unless otherwise stated, we will assume that $p=\operatorname {char}(\mathbb {F}_q)>3$ .

We will study the curve C by first finding the singular points, and then checking that C is irreducible. Finally, we will prove that C is tangent-filling, establishing Theorem 1.3.

3.1 Rational points of the curve

We start by finding all the $\mathbb {F}_q$ -points on C.

Lemma 3.2. The set $C(\mathbb {F}_q)$ is equal to the set of all points $[x:y:z]\in \mathbb {P}^2(\mathbb {F}_q)$ such that

$$ \begin{align*} xyz(x+y+z)\neq 0. \end{align*} $$

Proof. Since $x^{q-1} = 1$ holds for every $x\in \mathbb {F}_q^{\ast }$ , the conclusion is clear from (3.3).

Corollary 3.3. The curve C is not blocking.

Proof. Consider the $\mathbb {F}_q$ -line $L=\{z=0\}$ . Then $C\cap L$ has no $\mathbb {F}_q$ -points due to the condition in Lemma 3.2. Thus, $C(\mathbb {F}_q)$ is not a blocking set.

3.2 Singular points of the curve

Our goal is to determine the singular points of the curve C over $\overline {\mathbb {F}_q}$ .

Proposition 3.4. The curve C has only one singular point, namely $[1:1:1]$ .

Proof. By looking at the partial derivatives of the defining polynomial in (3.3), any singular point $[x_0:y_0:z_0]$ of C must satisfy,

(3.4) $$ \begin{align} x_0^{q-2}=y_0^{q-2}=z_0^{q-2}=3(x_0+y_0+z_0)^{q-2}. \end{align} $$

In particular, any singular point $[x_0:y_0:z_0]\in C(\overline {\mathbb {F}_q})$ satisfies

(3.5) $$ \begin{align} x_0y_0z_0(x_0+y_0+z_0)\ne 0. \end{align} $$

So, without loss of generality, we may assume that $z_0=1$ . Thus, a potential singular point takes the form $[x_0:y_0:1]$ and satisfies $x_0y_0\neq 0$ by Equation (3.5). Applying (3.4), we get

(3.6) $$ \begin{align} x_0^{q-2} = y_0^{q-2} = 3(x_0+y_0+1)^{q-2} = 1. \end{align} $$

We begin by computing

(3.7) $$ \begin{align} (x_0+y_0+1)^{q-2} = \frac{(x_0+y_0+1)^{q}}{(x_0+y_0+1)^2} = \frac{1+x_0^q + y_0^q}{(1+x_0+y_0)^2}. \end{align} $$

Equations (3.6) and (3.7) together give

(3.8) $$ \begin{align} \frac{3+3x_0^2+3y_0^2}{(1+x_0+y_0)^2} = 1. \end{align} $$

We can rearrange (3.8) as $x_0^2+y_0^2 - x_0 y_0 - x_0 - y_0 + 1 = 0$ , which can be expressed as an equation of degree $2$ in $y_0$ :

$$ \begin{align*} y_0^2 - y_0(x_0+1) + x_0^2-x_0+1 = 0. \end{align*} $$

Solving for $y_0$ , we obtain

(3.9) $$ \begin{align} y_0 = \frac{x_0+1 + (x_0-1)\gamma}{2}, \end{align} $$

where $\gamma $ satisfies $\gamma ^2 = -3$ . We compute $y_0^q$ using (3.9):

(3.10) $$ \begin{align} y_0^q = \frac{x_0^q+1 + (x_0^q-1)\gamma^q}{2}. \end{align} $$

We also compute $y_0^2$ using (3.9):

$$ \begin{align*} y_0^2 = \frac{(x_0^2+2x_0+1)+2(x_0+1)(x_0-1)\gamma + (x_0^2-2x_0+1)\cdot (-3)}{4}, \end{align*} $$

which simplifies to

(3.11) $$ \begin{align} y_0^2 = \frac{-x_0^2 + 4x_0 - 1 + (x_0^2-1)\gamma}{2}. \end{align} $$

Since $y_0^{q-2}=1$ by (3.6), we know that $y_0^q = y_0^{2}$ . Equating (3.10) and (3.11),

(3.12) $$ \begin{align} \frac{-x_0^2 + 4x_0 - 1 + (x_0^2-1)\gamma}{2} = \frac{x_0^q+1 + (x_0^q-1)\gamma^q}{2}. \end{align} $$

We proceed by analysing two cases, depending on whether $\gamma \in \mathbb {F}_q$ or $\gamma \notin \mathbb {F}_q$ .

Case 1: $\gamma \in \mathbb {F}_q$ . In this case, we have $\gamma ^q = \gamma $ . Using $x_0^{q}=x_0^{2}$ which is implied by (3.6), Equation (3.12) yields

$$ \begin{align*} \frac{-x_0^2 + 4x_0 - 1 + (x_0^2-1)\gamma}{2} = \frac{x_0^2+1 + (x_0^2-1)\gamma}{2}, \end{align*} $$

which simplifies to $(x_0-1)^2=0$ and so $x_0=1$ . Using (3.9), we obtain $y_0=1$ as well. This results in the singular point $[1:1:1]$ of the curve C.

Case 2: $\gamma \notin \mathbb {F}_q$ . In this case, $\gamma \in \mathbb {F}_{q^2}\setminus \mathbb {F}_q$ because $\gamma ^2=-3$ . Since $\gamma ^{q}$ is the Galois conjugate of $\gamma $ , we have $\gamma ^{q}=-\gamma $ . Thus, (3.12) yields

$$ \begin{align*} \frac{-x_0^2 + 4x_0 - 1 + (x_0^2-1)\gamma}{2} = \frac{x_0^q+1 - (x_0^q-1)\gamma}{2}. \end{align*} $$

This simplifies (due to $x_0^q=x_0^2$ ) to

$$ \begin{align*} (x_0-1)^2 = (x_0^2-1)\gamma. \end{align*} $$

We can eliminate the case $x_0=1$ because that will only bring us back to the singular point $[1:1:1]$ already analysed in the previous case. After dividing both sides of the preceding equation by $x_0-1$ and solving for $x_0$ , we get

(3.13) $$ \begin{align} x_0 = \frac{1+\gamma}{1-\gamma}. \end{align} $$

Using the relation $\gamma ^2=-3$ , formula (3.13) simplifies to

(3.14) $$ \begin{align} x_0 = \frac{\gamma-1}{2}. \end{align} $$

Applying (3.9), we obtain

(3.15) $$ \begin{align} y_0 = \frac{-\gamma-1}{2}. \end{align} $$

Since $\gamma ^2=-3$ , we have two solutions (once $\gamma $ is chosen, $-\gamma $ is also a solution). Thus, (3.14) and (3.15) allow us to conclude that there are two potential singular points on the curve C:

$$ \begin{align*} \bigg[\frac{\gamma-1}{2} : \frac{-\gamma-1}{2}: 1 \bigg] \quad \text{and} \quad \bigg[\frac{-\gamma-1}{2} : \frac{\gamma-1}{2}: 1 \bigg]. \end{align*} $$

However, both of these points satisfy $x_0+y_0+1=0$ . By Equation (3.5), neither of these two points is singular on the curve C.

We conclude that Case 2 does not occur after all and the point $[1:1:1]$ is the unique singular point of C.

3.3 Irreducibility of the curve

We begin with a general irreducibility criterion for a plane curve of degree at least $3$ with a unique singular point.

Lemma 3.5. Suppose that $D=\{F=0\}$ is a plane curve defined over a field K with $\deg (F)\geq 3$ and a unique singular point $P_0\in D(\overline {K})$ . After dehomogenising $f(x,y) := F(x, y, 1)$ and applying translation, we may assume that $(0, 0)$ is the singular point of the affine curve $\{f=0\}$ . Assume that the quadratic term $A_2(x, y)$ in the expansion of f around $(0, 0)$ cannot be written as $L(x,y)^2$ for some $L(x,y)\in \overline {K}[x,y]$ (in other words, the equation $A_2(x,y)=0$ has precisely two solutions in $\mathbb {P}^1(\overline {K})$ ). Then the plane curve D is irreducible over $\overline {K}$ .

Proof. Since $(0, 0)$ is a singular point of $\{f=0\}$ , we can then express

$$ \begin{align*} f(x,y) = A_2(x,y) + A_3(x,y) + \cdots \end{align*} $$

where $A_i(x,y)$ is a homogeneous polynomial of degree i in x and y. By hypothesis, $A_2(x,y)$ splits over $\overline {K}$ as a product $L_1(x,y)\cdot L_2(x,y)$ of two distinct nonzero linear forms. If $f(x, y)=g(x, y)\cdot h(x, y)$ where $g(0,0)=h(0,0)=0$ , then we claim that the component curves $\{g=0\}$ and $\{h=0\}$ meet at the point $(0,0)$ with multiplicity $1$ . Indeed, the expansions of $g(x,y)$ and $h(x,y)$ around the origin $(0,0)$ must necessarily take the form (after multiplication by a suitable nonzero constant)

$$ \begin{align*} g(x,y) = L_1(x,y) + B_2(x,y) + B_3(x,y) + \cdots \end{align*} $$

and

$$ \begin{align*} h(x,y) = L_2(x,y) + C_2(x,y) + C_3(x,y) + \cdots \end{align*} $$

respectively, where $B_i(x,y)$ and $C_i(x,y)$ are homogeneous polynomials of degree i in x and y. Since $L_1(x,y)$ and $L_2(x,y)$ are distinct linear forms which generate the maximal ideal of $\overline {K}[x,y]$ at $(0,0)$ , the two curves $\{g=0\}$ and $\{h=0\}$ meet with multiplicity $1$ at $(0,0)$ .

We show that the plane curve $D=\{F=0\}$ is irreducible over $\overline {K}$ . Assume, to the contrary, that $F=G\cdot H$ for some homogeneous polynomials G and H with positive degrees $d_1$ and $d_2$ , respectively. Let $g(x,y) := G(x, y, 1)$ and $h(x, y) := H(x, y, 1)$ . After applying Bézout’s theorem, $d_1 d_2$ intersection points (counted with multiplicity) of $\{G=0\}$ and $\{H=0\}$ must be singular points of D. Since D has a unique singular point, namely $(0, 0)$ in the affine chart $z=1$ , the local intersection multiplicity at the origin must be at least $d_1 d_2 \geq 2$ . This contradicts the fact that $\{g=0\}$ and $\{h=0\}$ meet with multiplicity exactly $1$ at $(0, 0)$ .

Proposition 3.6. The curve C defined by (3.3) is geometrically irreducible.

Proof. By Proposition 3.4, the curve C has the unique singular point $[1:1:1]$ . Expanding the equation $x^{q-1}+y^{q-1}+1-3(x+y+1)^{q-1}=0$ around the point $(1, 1)$ , we are led to analyse

$$ \begin{align*} (1 + (x-1))^{q-1} + (1 + (y-1))^{q-1} + 1 - 3(3 + (x-1) + (y-1))^{q-1}. \end{align*} $$

After expanding, the first nonzero homogeneous form in $(x-1)$ and $(y-1)$ has degree $2$ and is given by

$$ \begin{align*} 2\cdot 3^{q-2}\cdot [(x-1)^2 - (x-1)(y-1) + (y-1)^2 ]. \end{align*} $$

Since the discriminant of the quadratic $s^2-st+t^2$ is $-3\neq 0$ in $\mathbb {F}_q$ , the hypothesis of Lemma 3.5 is satisfied. Thus, C is irreducible over $\overline {\mathbb {F}_q}$ .

3.4 Tangent-filling property

In this final subsection, we give the proof that the curve C defined by (3.3) is tangent-filling over $\mathbb {F}_q$ .

Proof of Theorem 1.3.

Let $P=[a_0:b_0:c_0]$ be an arbitrary point in $\mathbb {P}^2(\mathbb {F}_q)$ . We want to find a smooth $\mathbb {F}_q$ -point $Q=[x_0:y_0:z_0]$ of C such that P is contained in the tangent line $T_Q C$ . From Lemma 3.2, an $\mathbb {F}_q$ -point $[x_0:y_0:z_0]$ is a point on the curve C if and only if

(3.16) $$ \begin{align} x_0y_0z_0(x_0+y_0+z_0)\neq 0. \end{align} $$

Note that P is contained in the tangent line $T_Q C$ if and only if

(3.17) $$ \begin{align} a_0\cdot (3 s_0^{q-2}-x_0^{q-2})+ b_0\cdot (3s_0^{q-2}-y_0^{q-2})+ c_0\cdot (3s_0^{q-2} - z_0^{q-2})=0, \end{align} $$

where $s_0=x_0+y_0+z_0$ . Since $s^{q-1}=1$ for each $s\in \mathbb {F}_q^{\ast }$ , we rewrite (3.17) as

(3.18) $$ \begin{align} \frac{3(a_0+b_0+c_0)}{x_0+y_0+z_0}=\frac{a_0}{x_0}+\frac{b_0}{y_0} +\frac{c_0}{z_0}. \end{align} $$

Note that all the denominators in (3.18) are nonzero because Lemma 3.2 guarantees that $xyz(x+y+z)\neq 0$ for any $\mathbb {F}_q$ -point $[x:y:z]$ of the curve C.

Case 1. Suppose $a_0b_0c_0(a_0+b_0+c_0)\ne 0$ and $[a_0:b_0:c_0]\ne [1:1:1]$ .

In this case, the point $P=[a_0:b_0:c_0]$ is already smooth in $C(\mathbb {F}_q)$ by Lemma 3.2 and Proposition 3.4. Hence, we may take $Q=P$ because P always belongs to $T_P C$ .

Case 2. Suppose $a_0+b_0+c_0=0$ .

In this case, (3.18) yields

(3.19) $$ \begin{align} \frac{a_0}{x_0}+\frac{b_0}{y_0}+\frac{c_0}{z_0}=0. \end{align} $$

We search for a solution $[x_0:y_0:z_0]\ne [1:1:1]$ satisfying (3.16).

Subcase 2.1. $a_0+b_0+c_0=0$ and $a_0b_0c_0\ne 0$ .

Since $\operatorname {char}(\mathbb {F}_q)>3$ , we cannot have $a_0=b_0=c_0$ . We may assume, without loss of generality, that $b_0\ne c_0$ . Let $z_0=1$ and $y_0=-1$ , and solve for $x_0$ according to Equation (3.19):

$$ \begin{align*} x_0=\frac{a_0}{b_0-c_0}\in \mathbb{F}_q^{\ast}. \end{align*} $$

Clearly, $[x_0:y_0:z_0]\ne [1:1:1]$ and (3.16) is satisfied.

Subcase 2.2. $a_0+b_0+c_0=0$ and $a_0b_0c_0=0$ .

By symmetry, we may assume that $a_0 = 0$ ; since $a_0 + b_0 + c_0 = 0$ , we have ${[a_0 : b_0 : c_0]= [0:1:-1]}$ , and so Equation (3.19) yields $y_0=z_0$ . The point ${[x_0:y_0:z_0]=[2:1:1]}$ satisfies both (3.16) and (3.19). This concludes our proof that all points $[a_0:b_0:c_0]$ for which $a_0+b_0+c_0=0$ belong to a tangent line at a smooth $\mathbb {F}_q$ -point of C.

Case 3. $a_0+b_0+c_0\neq 0$ and $a_0b_0c_0=0$ .

Since we seek points $[x_0:y_0:z_0]$ with $x_0+y_0+z_0\neq 0$ , we can scale $[a_0:b_0:c_0]$ and $[x_0:y_0:z_0]$ so that

$$ \begin{align*} a_0 + b_0 + c_0 = 3 \quad \text{and} \quad x_0+y_0+z_0=9. \end{align*} $$

Equation (3.18) now reads

(3.20) $$ \begin{align} 1=\frac{a_0}{x_0}+\frac{b_0}{y_0}+\frac{3-a_0-b_0}{9-x_0-y_0}. \end{align} $$

Since $a_0b_0c_0=0$ , we may assume by symmetry that $a_0=0$ . As a result, (3.20) reads

(3.21) $$ \begin{align} 1=\frac{b_0}{y_0} + \frac{3-b_0}{z_0}. \end{align} $$

If $b_0\notin \{0,-3,3\}$ , then we let $z_0=6$ , $y_0=6b_0/(3+b_0)$ and $x_0=(9-3b_0)/(3+b_0)$ . Note that $[x_0:y_0:z_0]\neq [1:1:1]$ and satisfies both (3.21) and (3.16).

If $b_0=0$ , then we simply choose $[x_0:y_0:z_0]=[2:4:3]\neq [1:1:1]$ which satisfies both (3.21) and (3.16).

If $b_0=-3$ , then we get the solution $[x_0:y_0:z_0]=[-1:6:4]\ne [1:1:1]$ which satisfies both (3.21) and (3.16).

If $b_0=3$ , then we get the solution $[x_0:y_0:z_0]=[2:3:4]\ne [1:1:1]$ which satisfies both (3.21) and (3.16).

Case 4. $[a_0:b_0:c_0]=[1:1:1]$ .

We can assume $a_0=b_0=c_0=1$ , and also $x_0+y_0+z_0=9$ after scaling ${[x_0:y_0:z_0]}$ . Then Equation (3.18) yields

(3.22) $$ \begin{align} 1=\frac{1}{x_0}+\frac{1}{y_0}+\frac{1}{9-x_0-y_0}. \end{align} $$

Our goal is to find a solution $(3,3)\neq (x_0,y_0)\in \mathbb {F}_q^*\times \mathbb {F}_q^*$ to (3.22).

After multiplying (3.22) by $x_0y_0(9-x_0-y_0)$ , we obtain

$$ \begin{align*} 9x_0y_0-x_0^2y_0-x_0y_0^2=9y_0-x_0y_0-y_0^2+9x_0-x_0^2-x_0y_0+x_0y_0, \end{align*} $$

which we rearrange as

$$ \begin{align*} y_0^2(x_0-1)+y_0(x_0-1)(x_0-9)-x_0(x_0-9)=0. \end{align*} $$

Our goal is to show that the number of $\mathbb {F}_q$ -points on the affine curve Y given by the equation

(3.23) $$ \begin{align} y^2(x-1)+y(x-1)(x-9)-x(x-9)=0 \end{align} $$

is strictly more than the number of points which we want to avoid from the set

(3.24) $$ \begin{align} \{(0,9), (0,0), (9,0), (3,3)\}. \end{align} $$

Indeed, besides the point $(3,3)$ , the points $(x_0,y_0)$ on the curve given by (3.23) which we have to avoid are the ones satisfying the equation

$$ \begin{align*}x_0y_0\cdot (x_0+y_0-9)=0.\end{align*} $$

We note that there are only three such points on the curve (3.23): $(0,0)$ , $(0,9)$ and $(9,0)$ ; this follows easily from Equation (3.23) after substituting either $x=0$ , or $y=0$ , or $x=9-y$ .

Now, for each $\mathbb {F}_q$ -point $(x_0,w_0)\ne (1,0)$ on the affine conic $\tilde {Y}$ given by the equation

$$ \begin{align*}w^2=(x-1)(x-9),\end{align*} $$

we have the $\mathbb {F}_q$ -point $(x_0,y_0)$ on Y given by

(3.25) $$ \begin{align} (x_0,y_0) := \bigg(x_0,\frac{-(x_0-1)(x_0-9)+(x_0-3)w_0}{2(x_0-1)}\bigg). \end{align} $$

Since there are $q-2$ points $(x_0,w_0)\ne (1,0)$ on $\tilde {Y}(\mathbb {F}_q)$ (because we have $q+1$ points on its projective closure in $\mathbb {P}^2$ and only two such points are on the line at infinity), we obtain $(q-2)\ \mathbb {F}_q$ -points on Y. Note that if $(x_1,w_1)\ne (x_0,w_0)$ are distinct points on $\tilde {Y}(\mathbb {F}_q)\setminus \{(1,0)\}$ , then the corresponding points on $Y(\mathbb {F}_q)$ are also distinct unless $x_0=x_1=3$ as can be seen from (3.25). There are at most two points on $\tilde {Y}(\mathbb {F}_q)$ having x-coordinate equal to $3$ (which in fact happens when $q=7$ , in which case $(3,\pm 3)\in \tilde {Y}(\mathbb {F}_7)$ ). Thus, we are guaranteed to have at least $q-3$ distinct points in $Y(\mathbb {F}_q)$ . Hence, as long as $q>7$ , we are guaranteed to avoid the points listed in (3.24).

Therefore, the curve C is tangent-filling when $q>7$ and $\operatorname {char}(\mathbb {F}_q)>3$ .

Remark 3.7. The result in Theorem 1.3 is sharp in the sense that when $q=7$ , the curve $x^{q-1}+y^{q-1}+z^{q-1}-3(x+y+z)^{q-1}=0$ is not tangent-filling. Indeed, one can check that for the point $P=[1:1:1]$ , there is no smooth $\mathbb {F}_7$ -point Q on this curve C such that $P\in T_Q C$ .