Article contents
SUMS OF FOUR SQUARES WITH A CERTAIN RESTRICTION
Published online by Cambridge University Press: 14 January 2021
Abstract
Z.-W. Sun [‘Refining Lagrange’s four-square theorem’, J. Number Theory175 (2017), 169–190] conjectured that
every positive integer n can be written as 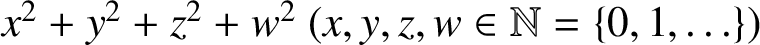 $ x^2+y^2+z^2+w^2\ (x,y,z,w\in \mathbb {N}=\{0,1,\ldots \})$
with
$ x^2+y^2+z^2+w^2\ (x,y,z,w\in \mathbb {N}=\{0,1,\ldots \})$
with
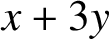 $x+3y$
a square and also as
$x+3y$
a square and also as
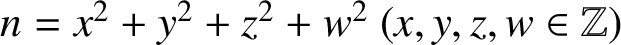 $n=x^2+y^2+z^2+w^2\ (x,y,z,w \in \mathbb {Z})$
with
$n=x^2+y^2+z^2+w^2\ (x,y,z,w \in \mathbb {Z})$
with
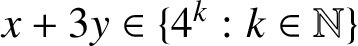 $x+3y\in \{4^k:k\in \mathbb {N}\}$
. In this paper, we confirm these conjectures via the arithmetic theory of ternary quadratic forms.
$x+3y\in \{4^k:k\in \mathbb {N}\}$
. In this paper, we confirm these conjectures via the arithmetic theory of ternary quadratic forms.
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 104 , Issue 2 , October 2021 , pp. 218 - 227
- Copyright
- © 2021 Australian Mathematical Publishing Association Inc.
Footnotes
This research was supported by the National Natural Science Foundation of China (grant no. 11971222). The second author was supported by NUPTSF (grant no. NY220159).
References
- 1
- Cited by



