Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kim, Byeong Moon
and
Kim, Ji Young
2017.
Sums of nonvanishing integral squares in real quadratic fields.
Journal of Number Theory,
Vol. 177,
Issue. ,
p.
497.


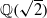 ,
, 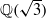 AND
AND 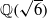
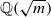 which can be represented as sums of distinct integral squares, where
which can be represented as sums of distinct integral squares, where 