Hostname: page-component-6bf8c574d5-7jkgd Total loading time: 0 Render date: 2025-02-20T07:53:36.885Z Has data issue: false hasContentIssue false
  • English
  • Français

STRONGLY 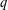$q$-ADDITIVE FUNCTIONS AND DISTRIBUTIONAL PROPERTIES OF THE LARGEST PRIME FACTOR

Part of: Exponential sums and character sums Elementary number theory Multiplicative number theory

Published online by Cambridge University Press:  17 November 2015

M. AMRI ,
M. MKAOUAR  and
W. WANNES
M. AMRI
Affiliation:
Faculté des Sciences de Sfax, BP 1171, Sfax 3000, Tunisie email [email protected]
M. MKAOUAR*
Affiliation:
Faculté des Sciences de Sfax, BP 1171, Sfax 3000, Tunisie email [email protected]
W. WANNES
Affiliation:
Faculté des Sciences de Sfax, BP 1171, Sfax 3000, Tunisie email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 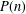$P(n)$ denote the largest prime factor of an integer 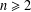$n\geq 2$. In this paper, we study the distribution of the sequence 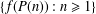$\{f(P(n)):n\geq 1\}$ over the set of congruence classes modulo an integer 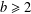$b\geq 2$, where 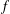$f$ is a strongly 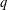$q$-additive integer-valued function (that is, 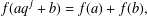$f(aq^{j}+b)=f(a)+f(b),$ with 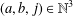$(a,b,j)\in \mathbb{N}^{3}$, 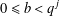$0\leq b<q^{j}$). We also show that the sequence 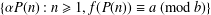$\{{\it\alpha}P(n):n\geq 1,f(P(n))\equiv a\;(\text{mod}~b)\}$ is uniformly distributed modulo 1 if and only if 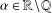${\it\alpha}\in \mathbb{R}\!\setminus \!\mathbb{Q}$.

Keywords

largest prime factorq-additive functionuniform distribution modulo 1

MSC classification

Primary: 11A63: Radix representation; digital problems
Secondary: 11L03: Trigonometric and exponential sums, general 11N05: Distribution of primes
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 93 , Issue 2 , April 2016 , pp. 177 - 185
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Banks, W., Harman, G. and Shparlinski, I. E., ‘Distributional properties of the largest prime factor’, Michigan Math. J. 53 (2005), 665–681.Google Scholar
Bellman, R. and Shapiro, H. N., ‘A problem in additive number theory’, Ann. of Math. (2) 49 (1948), 333–340.Google Scholar
Coquet, J., ‘Sur les fonctions Q-multiplicatives et Q-additives’, Thèse $3\grave{e} me$ cycle, Orsay, 1975.Google Scholar
de La Vallée Poussin, C. J., ‘Recherches analytiques sur la théorie des nombres premiers’, Ann. Soc. Sci. Bruxelles 21 (1896), 183–256 and 281–397.Google Scholar
Hadamard, J., ‘Sur la distribution des zéros de la fonction 𝜁(s) et ses conséquences arithmétiques’, Bull. Soc. Math. France 24 (1896), 199–220.Google Scholar
Ivić, A., ‘On sums involving reciprocals of the largest prime factor of an integer II’, Acta. Arith. 75 (1995), 229–251.Google Scholar
Kuipers, L. and Niederreiter, H., Uniform Distribution of Sequences (John Wiley, New York, 1974).Google Scholar
Landau, E., Handbuch der Lehre von der Verteilung der Primzahlen (Teubner, Leipzig, 1909).Google Scholar
Landau, E., ‘Über die 𝜁-function und die L-funktionen’, Math. Z. 20 (1924), 105–125.CrossRefGoogle Scholar
Martin, B., Mauduit, C. and Rivat, J., ‘Théorème des nombres premiers pour les fonctions digitales’, Acta. Arith. 165 (2014), 11–45.CrossRefGoogle Scholar
Mauduit, C. and Sárközy, A., ‘On the arithmetic structure of sets characterized by sum of digits properties’, J. Number Theory 61 (1996), 25–38.CrossRefGoogle Scholar
Mkaouar, M., Ouled Azaiz, N. and Thuswaldner, J., ‘Sur les chiffres des nombres premiers translatés’, Funct. Approx. Comment. Math. 51 (2014), 237–267.Google Scholar
Oon, S. M., ‘Pseudorandom properties of prime factors’, Period. Math. Hungar. 49 (2004), 45–63.Google Scholar
Tenenbaum, G., Introduction to Analytic and Probabilistic Number Theory (Cambridge University Press, Cambridge, 1995).Google Scholar
Vinogradov, I. M., The Method of Trigonometrical Sums in the Theory of Numbers (Dover, Mineola, NY, 2004).Google Scholar