Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T13:07:31.979Z Has data issue: false hasContentIssue false
  • English
  • Français

THE STRONG IRREDUCIBILITY OF A CLASS OF COWEN–DOUGLAS OPERATORS ON BANACH SPACES

Part of: Special classes of linear operators General theory of linear operators

Published online by Cambridge University Press:  16 August 2016

LIQIONG LIN  and
YUNNAN ZHANG
LIQIONG LIN
Affiliation:
College of Mathematics and Computer Science, Fuzhou University, Fuzhou 350117, China email [email protected]
YUNNAN ZHANG*
Affiliation:
School of Mathematics and Computer Science, Fujian Normal University, Fuzhou 350117, China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 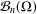${\mathcal{B}}_{n}(\unicode[STIX]{x1D6FA})$ be the set of Cowen–Douglas operators of index $n$ on a nonempty bounded connected open subset 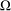$\unicode[STIX]{x1D6FA}$ of 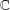$\mathbb{C}$. We consider the strong irreducibility of a class of Cowen–Douglas operators 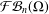${\mathcal{F}}{\mathcal{B}}_{n}(\unicode[STIX]{x1D6FA})$ on Banach spaces. We show 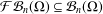${\mathcal{F}}{\mathcal{B}}_{n}(\unicode[STIX]{x1D6FA})\subseteq {\mathcal{B}}_{n}(\unicode[STIX]{x1D6FA})$ and give some conditions under which an operator 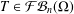$T\in {\mathcal{F}}{\mathcal{B}}_{n}(\unicode[STIX]{x1D6FA})$ is strongly irreducible. All these results generalise similar results on Hilbert spaces.

Keywords

Cowen–Douglas operatorsstrongly irreducible operatorsRosenblum operatorsBanach spaces

MSC classification

Primary: 47A05: General (adjoints, conjugates, products, inverses, domains, ranges, etc.)
Secondary: 47B32: Operators in reproducing-kernel Hilbert spaces (including de Branges, de Branges-Rovnyak, and other structured spaces)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 94 , Issue 3 , December 2016 , pp. 479 - 488
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Cowen, M. J. and Douglas, R. G., ‘Complex geometry and operator theory’, Acta Math. 141 (1978), 187–261.Google Scholar
Gilfeather, F., ‘Strong reducibility of operators’, Indiana Univ. Math. J. 22 (1972), 97–133.Google Scholar
Herrero, D. A., ‘An essay on quasisimilarity’, in: Operator Theory: Advances and Applications, Vol. 18 (Birkhauser, Basel, 1988), 125–154.Google Scholar
Ji, K., Jiang, C. L., Keshari, D. K. and Misra, G., ‘Flag structure for operators in the Cowen–Douglas class’, C. R. Math. Acad. Sci. Paris 352(6) (2014), 511–514.CrossRefGoogle Scholar
Ji, K., Jiang, C. L., Keshari, D. K. and Misra, G., ‘Rigidity of the flag structure for a class of Cowen–Douglas operators’, arXiv:1405.3874v1 (2014), 27 pages.Google Scholar
Jiang, C. L., Guo, X. Z. and Ji, K., ‘ K-group and similarity classification of operators’, J. Funct. Anal. 225 (2005), 167–192.CrossRefGoogle Scholar
Jiang, C. L. and Ji, K., ‘Similarity classification of holomorphic curves’, Adv. Math. 215 (2007), 446–468.Google Scholar
Jiang, Z. J. and Sun, S. L., ‘On completely irreducible operators’, Acta. Sci. Natur. Univ. Jilin 4 (1992), 20–29 (in Chinese).Google Scholar
Jiang, C. L. and Wang, Z. Y., Strongly Irreducible Operators on Hilbert Space (Longman, Harlow, 1998).Google Scholar
Jiang, C. L. and Wang, Z. Y., Structure of Hilbert Space Operators (World Scientific Printers, Singapore, 2006).Google Scholar
Kleinecke, D. C., ‘On operator commutator’, Proc. Amer. Math. Soc. 8 (1957), 535–536.Google Scholar
Zhang, Y. N. and Zhong, H. J., ‘Strongly irreducible operators and Cowen–Douglas operators on c 0, l p (1 ≤ p < ∞)’, Front. Math. China 6(5) (2011), 987–1001.CrossRefGoogle Scholar