Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T22:23:43.782Z Has data issue: false hasContentIssue false
  • English
  • Français

THE STRICT TOPOLOGY ON THE DISCRETE LEBESGUE SPACES

Part of: Topological linear spaces and related structures Topological algebras, normed rings and algebras, Banach algebras

Published online by Cambridge University Press:  06 December 2010

SAEID MAGHSOUDI  and
RASOUL NASR-ISFAHANI
SAEID MAGHSOUDI*
Affiliation:
Department of Mathematics, Zanjan University, Zanjan, 313, Iran Research Institute for Fundamental Science, Tabriz, Iran (email: [email protected])
RASOUL NASR-ISFAHANI
Affiliation:
Department of Mathematical Sciences, Isfahan University of Technology, Isfahan, 84156-83111, Iran (email: [email protected])
*
✉For correspondence; e-mail: s˙[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Σ be a set and σ be a positive function on Σ. We introduce and study a locally convex topology β1(Σ,σ) on the space ℓ1(Σ,σ) such that the strong dual of (ℓ1(Σ,σ),β1(Σ,σ)) can be identified with the Banach space 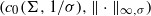. We also show that, except for the case where Σ is finite, there are infinitely many such locally convex topologies on ℓ1(Σ,σ). Finally, we investigate some other properties of the locally convex space (ℓ1(Σ,σ),β1(Σ,σ)) , and as an application, we answer partially a question raised by A. I. Singh [‘L∞0(G)* as the second dual of the group algebra L1 (G) with a locally convex topology’, Michigan Math. J.46 (1999), 143–150].

Keywords

discrete Lebesgue spacelocally convex spacestrict topologystrong dual

MSC classification

Secondary: 46A03: General theory of locally convex spaces 46H05: General theory of topological algebras
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 83 , Issue 2 , April 2011 , pp. 241 - 255
Copyright
Copyright © Australian Mathematical Publishing Association Inc. 2010

References

[1]Buck, R. C., ‘Bounded continuous functions on a locally compact space’, Michigan Math. J. 5 (1958), 95–104.CrossRefGoogle Scholar
[2]Collins, H. S., ‘Strict, weighted, and mixed topologies and applications’, Adv. Math. 19 (1976), 207–237.CrossRefGoogle Scholar
[3]Dorroh, J. R., ‘The localization of the strict topology via bounded sets’, Proc. Amer. Math. Soc. 20 (1969), 413–414.CrossRefGoogle Scholar
[4]Ferrera, J. and Prieto, A., ‘The strict topology on spaces of bounded holomorphic functions’, Bull. Aust. Math. Soc. 49 (1994), 249–256.CrossRefGoogle Scholar
[5]Gulick, D., ‘Duality theory for the strict topology’, Studia Math. 49 (1974), 195–208.CrossRefGoogle Scholar
[6]Jarchow, H., Locally Convex Spaces (B. G. Teubner, Stuttgart, 1981).CrossRefGoogle Scholar
[7]Khan, L. A., The General Strict Topology on Topological Modules, Contemporary Mathematics, 435 (American Mathematical Society, Providence, RI, 2007), pp. 253–263.Google Scholar
[8]Robertson, J. M. and Wiser, H. C., ‘A note on polar topologies’, Canad. Math. Bull. 11 (1968), 607–609.CrossRefGoogle Scholar
[9]Ruess, W., ‘On the locally convex structure of strict topologies’, Math. Z. 153 (1977), 179–192.CrossRefGoogle Scholar
[10]Sentilles, F. and Taylor, D., ‘Factorization in Banach algebras and the general strict topology’, Trans. Amer. Math. Soc. 142 (1969), 141–152.CrossRefGoogle Scholar
[11]Shapiro, J. H., ‘The bounded weak star topology and the general strict topology’, J. Funct. Anal. 8 (1971), 275–286.CrossRefGoogle Scholar
[12]Singh, A. I., ‘L ∞0(G)* as the second dual of the group algebra L 1(G) with a locally convex topology’, Michigan Math. J. 46 (1999), 143–150.CrossRefGoogle Scholar
[13]Swartz, C., An Introduction to Functional Analysis, Pure and Applied Mathematics, 157 (Marcel Dekker, New York, 1992).Google Scholar
[14]Wheeler, R. F., ‘A survey of Baire measures and strict topologies’, Expo. Math. 1 (1983), 97–190.Google Scholar
[15]Wilansky, A., Modern Methods in Topological Vector Spaces (McGraw-Hill, New York, 1978).Google Scholar
[16]Zafarani, J., ‘A space of vector-valued measures and a strict topology’, Manuscripta Math. 39 (1982), 147–153.CrossRefGoogle Scholar