Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T12:22:19.507Z Has data issue: false hasContentIssue false
  • English
  • Français

SPACES OF SPECIAL QUADRILATERALS

Part of: Real and complex geometry General convexity Topological manifolds

Published online by Cambridge University Press:  07 January 2019

AHTZIRI GONZÁLEZ Open the ORCID record for AHTZIRI GONZÁLEZ [Opens in a new window]  and
JORGE L. LÓPEZ-LÓPEZ Open the ORCID record for JORGE L. LÓPEZ-LÓPEZ [Opens in a new window]
AHTZIRI GONZÁLEZ
Affiliation:
Centro de Ciencias Matemáticas, UNAM, Campus Morelia, C.P. 58190, Morelia, Michoacán, México email [email protected]
JORGE L. LÓPEZ-LÓPEZ*
Affiliation:
Facultad de Ciencias Físico-Matemáticas, Universidad Michoacana de San Nicolás de Hidalgo, Edificio Alfa, Ciudad Universitaria, C.P. 58040, Morelia, Michoacán, México email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We describe the parameter spaces of some families of quadrilaterals, such as parallelograms, rectangles, rhombuses, cyclic quadrilaterals and trapezoids. For this purpose, we prove that the closed $n$-disc 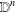$\mathbb{D}^{n}$ is the unique topological $n$-manifold (with boundary) whose boundary and interior are homeomorphic to 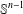$\mathbb{S}^{n-1}$ and 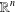$\mathbb{R}^{n}$, respectively. Roughly speaking, our main result states that the natural compactifications of the parameter spaces of cyclic quadrilaterals and of trapezoids, modulo similarity, are both homeomorphic to 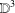$\mathbb{D}^{3}$.

Keywords

similarity classshapequadrilateral

MSC classification

Primary: 57N25: Shapes
Secondary: 51M99: None of the above, but in this section 52A10: Convex sets in $2$ dimensions (including convex curves)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 100 , Issue 1 , August 2019 , pp. 155 - 167
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

Footnotes

The first author is partially supported by CONACYT grant FORDECYT 265667; the second author is partially supported by funding from CIC-UMSNH.

References

Brown, M., ‘A proof of the generalized Schöenflies theorem’, Bull. Amer. Math. Soc. 66(2) (1960), 74–76.Google Scholar
Brown, M., ‘Locally flat imbeddings of topological manifolds’, Ann. of Math. (2) 75(2) (1962), 331–341.10.2307/1970177Google Scholar
González, A. and López-López, J. L., ‘Compactness of spaces of convex and simple quadrilaterals’, Bull. Aust. Math. Soc. 94(3) (2016), 507–521.10.1017/S0004972716000368Google Scholar
Hatcher, A., Algebraic Topology (Cambridge University Press, Cambridge, 2002).Google Scholar
Munkres, J. R., Topology (Prentice Hall, Upper Saddle River, NJ, 2000).Google Scholar