Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T10:48:38.078Z Has data issue: false hasContentIssue false
  • English
  • Français

SOME RESULTS ON THE DIFFERENCE OF THE ZAGREB INDICES OF A GRAPH

Part of: Graph theory

Published online by Cambridge University Press:  02 June 2015

MINGQIANG AN  and
LIMING XIONG
MINGQIANG AN*
Affiliation:
College of Science, Tianjin University of Science and Technology, Tianjin300457, PR China email [email protected]
LIMING XIONG
Affiliation:
School of Mathematics and Statistics, Beijing Institute of Technology, Beijing100081, PR China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The classical first and second Zagreb indices of a graph 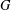$G$ are defined as 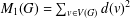$M_{1}(G)=\sum _{v\in V(G)}d(v)^{2}$ and 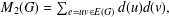$M_{2}(G)=\sum _{e=uv\in E(G)}d(u)d(v),$ where 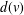$d(v)$ is the degree of the vertex $v$ of 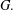$G.$ Recently, Furtula et al. [‘On difference of Zagreb indices’, Discrete Appl. Math.178 (2014), 83–88] studied the difference of 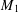$M_{1}$ and 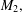$M_{2},$ and showed that this difference is closely related to the vertex-degree-based invariant 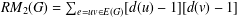$RM_{2}(G)=\sum _{e=uv\in E(G)}[d(u)-1][d(v)-1]$, the reduced second Zagreb index. In this paper, we present sharp bounds for the reduced second Zagreb index, given the matching number, independence number and vertex connectivity, and we also completely determine the extremal graphs.

Keywords

vertex degreeZagreb indexmatching numberindependence numbervertex connectivityextremal graphs

MSC classification

Primary: 05C35: Extremal problems
Secondary: 05C40: Connectivity 05C69: Dominating sets, independent sets, cliques 05C70: Factorization, matching, partitioning, covering and packing
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 92 , Issue 2 , October 2015 , pp. 177 - 186
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Balaban, A. T., Motoc, I., Bonchev, D. and Mekenyan, O., ‘Topological indices for structure–activity correlations’, Top. Curr. Chem. 114 (1983), 21–55.CrossRefGoogle Scholar
Bell, F. K., ‘A note on the irregularity of graphs’, Linear Algebra Appl. 161 (1992), 45–54.CrossRefGoogle Scholar
Bondy, J. A. and Murty, U. S. R., Graph Theory, Graduate Texts in Mathematics, 244 (Springer, New York, 2008).CrossRefGoogle Scholar
de Caen, D., ‘An upper bound on the sum of squares of degrees in a graph’, Discrete Math. 85 (1998), 245–248.CrossRefGoogle Scholar
Cioabǎ, S. M., ‘Sums of powers of the degrees of a graph’, Discrete Math. 306 (2006), 1959–1964.CrossRefGoogle Scholar
Das, K. C. and Gutman, I., ‘Some properties of the second Zagreb index’, MATCH Commun. Math. Comput. Chem. 52 (2004), 103–112.Google Scholar
Furtula, B., Gutman, I. and Ediz, S., ‘On difference of Zagreb indices’, Discrete Appl. Math. 178 (2014), 83–88.CrossRefGoogle Scholar
Gutman, I., ‘Degree-based topological indices’, Croat. Chem. Acta 86 (2013), 351–361.CrossRefGoogle Scholar
Gutman, I. and Das, K. C., ‘The first Zagreb index 30 years after’, MATCH Commun. Math. Comput. Chem. 50 (2004), 83–92.Google Scholar
Gutman, I., Furtula, B. and Elphick, C., ‘Three new/old vertex-degree-based topological indices’, MATCH Commun. Math. Comput. Chem. 72 (2014), 617–632.Google Scholar
Gutman, I., Rus̆c̆ić, B., Trinajstić, N. and Wilcox, C. F., ‘Graph theory and molecular orbitals, XII. Acyclic polyenes’, J. Chem. Phys. 62 (1975), 3399–3405.CrossRefGoogle Scholar
Gutman, I. and Trinajstić, N., ‘Graph theory and molecular orbitals, total 𝜋-electron energy of alternant hydrocarbons’, Chem. Phys. Lett. 17 (1972), 535–538.CrossRefGoogle Scholar
Hacke, J. E., ‘A simple solution of the general quartic’, Amer. Math. Monthly 48 (1941), 327–328.Google Scholar
Lovász, L. and Plummer, M. D., Matching Theory (American Mathematical Society, Chelsea, Providence, RI, 2009).Google Scholar
Milos̆evic̆, M., Réti, T. and Stevanović, D., ‘On the constant difference of Zagreb indices’, MATCH Commun. Math. Comput. Chem. 68 (2012), 157–168.Google Scholar
Nikolić, S., Kovac̆ević, G., Milic̆ević, A. and Trinajstić, N., ‘The Zagreb indices 30 years after’, Croat. Chem. Acta 76 (2003), 113–124.Google Scholar
Peled, U. N., Petreschi, R. and Sterbini, A., ‘(n, e)-graphs with maximum sum of squares of degrees’, J. Graph Theory 31 (1999), 283–295.3.0.CO;2-H>CrossRefGoogle Scholar
Tutte, W. T., ‘The factorization of linear graphs’, J. Lond. Math. Soc. (2) 22 (1947), 107–111.CrossRefGoogle Scholar
Vukičević, D. and Pisanski, T., ‘On the extremal values of the ratios of the number of paths’, Ars Math. Contemp. 3 (2010), 215–235.CrossRefGoogle Scholar