Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-08T17:38:08.575Z Has data issue: false hasContentIssue false
  • English
  • Français

SOME QUARTIC DIOPHANTINE EQUATIONS IN THE GAUSSIAN INTEGERS

Part of: Diophantine equations Arithmetic algebraic geometry

Published online by Cambridge University Press:  16 June 2015

FARZALI IZADI ,
RASOOL FOROOSHANI NAGHDALI  and
PETER GEOFF BROWN
FARZALI IZADI
Affiliation:
Department of Mathematics, Azarbaijan Shahid Madani University, Azar shahr, Tabriz, 53751-71379, Iran email [email protected]
RASOOL FOROOSHANI NAGHDALI*
Affiliation:
Department of Mathematics, Azarbaijan Shahid Madani University, Azar shahr, Tabriz, 53751-71379, Iran email [email protected]
PETER GEOFF BROWN
Affiliation:
School of Mathematics and Statistics, University of New South Wales, Sydney, NSW 2052, Australia email [email protected]
*
✉rn˙[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we examine solutions in the Gaussian integers to the Diophantine equation 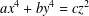$ax^{4}+by^{4}=cz^{2}$ for different choices of 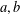$a,b$ and $c$. Elliptic curve methods are used to show that these equations have a finite number of solutions or have no solution.

Keywords

quartic Diophantine equationsGaussian integerselliptic curvesrankstorsion group

MSC classification

Primary: 11D25: Cubic and quartic equations
Secondary: 11G05: Elliptic curves over global fields
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 92 , Issue 2 , October 2015 , pp. 187 - 194
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Cohen, H., Number Theory: Vol. I: Tools and Diophantine Equations, Graduate Texts in Mathematics, 239 (Springer, New York, 2007).Google Scholar
Dickson, L. E., History of the Theory of Numbers, Vol. II: Diophantine Analysis (Chelsea, New York, 1971).Google Scholar
Mordell, L. J., Diophantine Equations (Academic Press, London, 1969).Google Scholar
Najman, F., ‘The Diophantine equation x 4 ± y 4 = iz 2 in the Gaussian integers’, Amer. Math. Monthly 117 (2010), 637–641.CrossRefGoogle Scholar
Schneiders, U. and Zimmer, H. G., ‘The rank of elliptic curves upon quadratic extensions’, in: Computational Number Theory (eds. Petho, A., Williams, H. C. and Zimmer, H. G.) (de Gruyter, Berlin, 1991), 239–260.Google Scholar
Silverman, J. H., The Arithmetic of Elliptic Curves (Springer, New York, 1986).CrossRefGoogle Scholar
Szabó, S., ‘Some fourth degree Diophantine equations in the Gaussian integers’, Integers 4 (2004), A16.Google Scholar