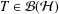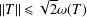Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hosseini, Mohsen Shah
and
Omidvar, Mohsen Erfanian
2018.
Some reverse and numerical radius inequalities.
Mathematica Slovaca,
Vol. 68,
Issue. 5,
p.
1121.
CAIN, BRYAN E.
2018.
IMPROVED INEQUALITIES FOR THE NUMERICAL RADIUS: WHEN INVERSE COMMUTES WITH THE NORM.
Bulletin of the Australian Mathematical Society,
Vol. 97,
Issue. 2,
p.
293.
Hosseini, Mohsen Shah
Moosavi, Baharak
and
Moradi, Hamid Reza
2020.
An alternative estimate for the numerical radius of Hilbert space operators.
Mathematica Slovaca,
Vol. 70,
Issue. 1,
p.
233.
Nikzat, Elham
and
Omidvar, Mohsen Erfanian
2022.
Refinements of numerical radius inequalities using the Kantorovich ratio.
Concrete Operators,
Vol. 9,
Issue. 1,
p.
70.
Moosavi, Baharak
and
Shah Hosseini, Mohsen
2023.
Norm and numerical radius inequalities for Hilbert space operators.
The Journal of Analysis,
Vol. 31,
Issue. 2,
p.
1393.