No CrossRef data available.
Published online by Cambridge University Press: 09 November 2020
Let
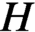 $ H $
be a compact subgroup of a locally compact group
$ H $
be a compact subgroup of a locally compact group
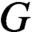 $ G $
. We first investigate some (operator) (co)homological properties of the Fourier algebra
$ G $
. We first investigate some (operator) (co)homological properties of the Fourier algebra
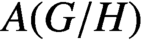 $A(G/H)$
of the homogeneous space
$A(G/H)$
of the homogeneous space
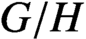 $G/H$
such as (operator) approximate biprojectivity and pseudo-contractibility. In particular, we show that
$G/H$
such as (operator) approximate biprojectivity and pseudo-contractibility. In particular, we show that
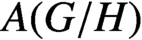 $ A(G/H) $
is operator approximately biprojective if and only if
$ A(G/H) $
is operator approximately biprojective if and only if
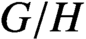 $ G/H $
is discrete. We also show that
$ G/H $
is discrete. We also show that
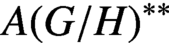 $A(G/H)^{**}$
is boundedly approximately amenable if and only if G is compact and H is open. Finally, we consider the question of existence of weakly compact multipliers on
$A(G/H)^{**}$
is boundedly approximately amenable if and only if G is compact and H is open. Finally, we consider the question of existence of weakly compact multipliers on
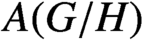 $A(G/H)$
.
$A(G/H)$
.
This research for the second author was in part supported by a grant from IPM (no. 99170411).