Article contents
Some fixed-point theorems on locally convex linear topological spaces
Published online by Cambridge University Press: 17 April 2009
Abstract
Let (E, τ) be a locally convex linear Hausdorff topological space. We have proved mainly the following results.
(i) Let f be nonexpansive on a nonempty τ-sequentially complete, τ-bounded, and starshaped subset M of E and let (I-f) map τ-bounded and τ-sequentially closed subsets of M into τ-sequentially closed subsets of M. Then f has a fixed-point in M.
(ii) Let f be nonexpansive on a nonempty, τ-sequentially compact, and starshaped subset M of E. Then f has a fixed-point in M.
(iii) Let (E, τ) be τ-quasi-complete. Let X be a nonempty, τ-bounded, τ-closed, and convex subset of E and M be a τ-compact subset of X. Let F be a commutative family of nonexpansive mappings on X having the property that for some f1 ∈ F and for each x ∈ X, τ-closure of the set
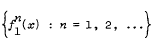
contains a point of M. Then the family F has a common fixed-point in M.
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 13 , Issue 2 , October 1975 , pp. 241 - 254
- Copyright
- Copyright © Australian Mathematical Society 1975
References
- 8
- Cited by


