Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T17:46:50.365Z Has data issue: false hasContentIssue false
  • English
  • Français

SOME EXTREMAL RESULTS ON THE CHROMATIC STABILITY INDEX

Part of: Graph theory

Published online by Cambridge University Press:  04 March 2022

SHENWEI HUANG Open the ORCID record for SHENWEI HUANG [Opens in a new window] ,
SANDI KLAVŽAR Open the ORCID record for SANDI KLAVŽAR [Opens in a new window] ,
HUI LEI Open the ORCID record for HUI LEI [Opens in a new window] ,
XIAOPAN LIAN Open the ORCID record for XIAOPAN LIAN [Opens in a new window]  and
YONGTANG SHI Open the ORCID record for YONGTANG SHI [Opens in a new window]
SHENWEI HUANG
Affiliation:
College of Computer Science, Nankai University, Tianjin 300350, China e-mail: [email protected]
SANDI KLAVŽAR*
Affiliation:
Faculty of Mathematics and Physics, University of Ljubljana, Ljubljana, Slovenia and Faculty of Natural Sciences and Mathematics, University of Maribor, Maribor, Slovenia and Institute of Mathematics, Physics and Mechanics, Ljubljana, Slovenia
HUI LEI
Affiliation:
School of Statistics and Data Science, LPMC and KLMDASR, Nankai University, Tianjin 300071, China e-mail: [email protected]
XIAOPAN LIAN
Affiliation:
Center for Combinatorics and LPMC, Nankai University, Tianjin, China e-mail: [email protected]
YONGTANG SHI
Affiliation:
Center for Combinatorics and LPMC, Nankai University, Tianjin, China e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The 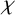$\chi $ -stability index 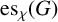$\mathrm {es}_{\chi }(G)$ of a graph G is the minimum number of its edges whose removal results in a graph with chromatic number smaller than that of G. We consider three open problems from Akbari et al. [‘Nordhaus–Gaddum and other bounds for the chromatic edge-stability number’, European J. Combin. 84 (2020), Article no. 103042]. We show by examples that a known characterisation of k-regular ( 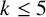$k\le 5$ ) graphs G with 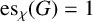$\mathrm {es}_{\chi }(G) = 1$ does not extend to 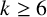$k\ge 6$ , and we characterise graphs G with 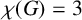$\chi (G)=3$ for which 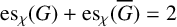$\mathrm { es}_{\chi }(G)+\mathrm {es}_{\chi }(\overline {G}) = 2$ . 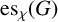We derive necessary conditions on graphs G which attain a known upper bound on $\mathrm { es}_{\chi }(G)$ in terms of the order and the chromatic number of G and show that the conditions are sufficient when 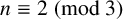$n\equiv 2 \pmod 3$ and 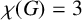$\chi (G)=3$ .

Keywords

chromatic numberchromatic stability indexregular graph

MSC classification

Primary: 05C15: Coloring of graphs and hypergraphs
Secondary: 05C35: Extremal problems
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 106 , Issue 2 , October 2022 , pp. 185 - 194
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Huang was partially supported by the National Natural Science Foundation of China (11801284) and the Fundamental Research Funds for the Central Universities, Nankai University. Lei, Lian and Shi were partially supported by the China–Slovenia bilateral project ‘Some topics in modern graph theory’ (No. 12-6), the National Natural Science Foundation of China and the Fundamental Research Funds for the Central Universities, Nankai University. Klavžar acknowledges the financial support from the Slovenian Research Agency (research core funding No. P1-0297 and projects J1-9109, J1-1693, N1-0095, N1-0108).

References

Akbari, S., Klavžar, S., Movarraei, N. and Nahvi, M., ‘Nordhaus–Gaddum and other bounds for the chromatic edge-stability number’, European J. Combin. 84 (2020), Article no. 103042.CrossRefGoogle Scholar
Alikhani, S. and Piri, M. R., ‘On the edge chromatic stability number of graphs’, Preprint, 2020, arXiv:2004.10551 [math.CO].Google Scholar
Arumugam, S., Sahul Hamid, I. and Muthukamatchi, A., ‘Independent domination and graph colorings’, in: Discrete Mathematics: Proceedings of the International Conference on Discrete Mathematics, Ramanujan Mathematical Society Lecture Notes, 7 (eds. Balakrishnan, R. and Madhavan, C.) (Ramanujan Mathematical Society, Mysore, 2008), 195–203.Google Scholar
Brešar, B., Klavžar, S. and Movarraei, N., ‘Critical graphs for the chromatic edge-stability number’, Discrete Math. 343 (2020), Article no. 111845.CrossRefGoogle Scholar
Dobrynin, A. A., Melnikov, L. S. and Pyatkin, A. V., ‘Regular $4$ -critical graphs of even degree’, J. Graph Theory 46 (2004), 103–130.CrossRefGoogle Scholar
Erdős, P., ‘Problem 9’, in: Theory of Graphs and Its Applications: Proceedings of the Symposium held in Smolenice, June 1963 (ed. Fiedler, M.) (Czech Academy of Sciences, Prague, 1964), 159.Google Scholar
Heckel, A., ‘Sharp concentration of the equitable chromatic number of dense random graphs’, Combin. Probab. Comput. 29 (2020), 213–233.CrossRefGoogle Scholar
Kemnitz, A., Marangio, M. and Movarraei, N., ‘On the chromatic edge stability number of graphs’, Graphs Combin. 34 (2018), 1539–1551.CrossRefGoogle Scholar
Li, M. and Zhang, X., ‘Relaxed equitable colourings of planar graphs with girth at least $\ 8$ ’, Discrete Math. 343 (2020), Article no. 111790.CrossRefGoogle Scholar
Staton, W., ‘Edge deletions and the chromatic number’, Ars Combin. 10 (1980), 103–106.Google Scholar