Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T08:06:44.040Z Has data issue: false hasContentIssue false
  • English
  • Français

SOME CONVERGENCE THEOREMS IN FOURIER ALGEBRAS

Part of: Commutative Banach algebras and commutative topological algebras Abstract harmonic analysis

Published online by Cambridge University Press:  03 July 2017

HEYBETKULU MUSTAFAYEV Open the ORCID record for HEYBETKULU MUSTAFAYEV [Opens in a new window]
HEYBETKULU MUSTAFAYEV*
Affiliation:
Department of Mathematics, Faculty of Science, Yuzuncu Yil University, Van, Turkey email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 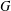$G$ be a locally compact amenable group and $A(G)$ and 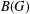$B(G)$ be the Fourier and the Fourier–Stieltjes algebras of 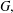$G,$ respectively. For a power bounded element $u$ of 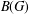$B(G)$, let 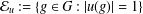${\mathcal{E}}_{u}:=\{g\in G:|u(g)|=1\}$. We prove some convergence theorems for iterates of multipliers in Fourier algebras.

(a) If 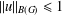$\Vert u\Vert _{B(G)}\leq 1$, then 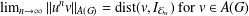$\lim _{n\rightarrow \infty }\Vert u^{n}v\Vert _{A(G)}=\text{dist}(v,I_{{\mathcal{E}}_{u}})\text{ for }v\in A(G)$, where 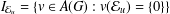$I_{{\mathcal{E}}_{u}}=\{v\in A(G):v({\mathcal{E}}_{u})=\{0\}\}$.

(b) The sequence 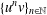$\{u^{n}v\}_{n\in \mathbb{N}}$ converges for every 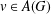$v\in A(G)$ if and only if 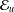${\mathcal{E}}_{u}$ is clopen and 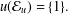$u({\mathcal{E}}_{u})=\{1\}.$

(c) If the sequence 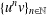$\{u^{n}v\}_{n\in \mathbb{N}}$ converges weakly in 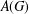$A(G)$ for some 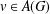$v\in A(G)$, then it converges strongly.

Keywords

locally compact groupFourier algebraFourier–Stieltjes algebraconvergence

MSC classification

Primary: 43A30: Fourier and Fourier-Stieltjes transforms on nonabelian groups and on semigroups, etc.
Secondary: 46J20: Ideals, maximal ideals, boundaries
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 96 , Issue 3 , December 2017 , pp. 487 - 495
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

References

Derighetti, A., ‘Some results on the Fourier–Stieltjes algebra of a locally compact group’, Comment. Math. Helv. 45 (1970), 219–228.Google Scholar
Derriennic, Y. and Lin, M., ‘Sur le comportement asymptotique des puissances de convolution d’une probabilité’, Ann. Inst. H. Poincaré 20 (1984), 127–132.Google Scholar
Eymard, P., ‘L’algébre de Fourier d’un groupe localement compact’, Bull. Soc. Math. France 92 (1964), 181–236.Google Scholar
Foguel, S. R., ‘On iterates of convolutions’, Proc. Amer. Math. Soc. 47 (1975), 368–370.Google Scholar
Forrest, B., Kaniuth, E., Lau, A. T. and Spronk, N., ‘Ideals with bounded approximate identities in Fourier algebras’, J. Funct. Anal. 203 (2003), 286–304.Google Scholar
Granirer, E. E., ‘On some properties of the Banach algebras A p (G) for locally compact groups’, Proc. Amer. Math. Soc. 95 (1985), 375–381.Google Scholar
Kaniuth, E., Lau, A. and Ülger, A., ‘Multipliers of commutative Banach algebras, power boundedness and Fourier–Stieltjes algebras’, J. Lond. Math. Soc. 81 (2010), 255–275.Google Scholar
Krengel, U., Ergodic Theorems (De Gruyter, Berlin, 1985).Google Scholar
Larsen, R., An Introduction to the Theory of Multipliers (Springer, New York, 1971).Google Scholar
Larsen, R., Banach Algebras (Marcel Dekker, New York, 1973).Google Scholar
Mustafayev, H., ‘Distance formulas in group algebras’, C. R. Acad. Sci. Paris 354 (2016), 577–582.Google Scholar