Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Shanmugam, T N
1986.
On a subclass of Bazilevic functions.
Proceedings of the Indian Academy of Sciences - Section A,
Vol. 95,
Issue. 2,
Özkan, Öznur
and
Altıntaş, Osman
2006.
Applications of differential subordination.
Applied Mathematics Letters,
Vol. 19,
Issue. 8,
p.
728.
Trojnar-Spelina, Lucyna
2008.
On certain applications of the Hadamard product.
Applied Mathematics and Computation,
Vol. 199,
Issue. 2,
p.
653.
Wang, Zhi-Gang
Jiang, Yue-Ping
and
Srivastava, H. M.
2008.
Some subclasses of multivalent analytic functions involving the Dziok–Srivastava operator.
Integral Transforms and Special Functions,
Vol. 19,
Issue. 2,
p.
129.
Al-Shaqsi, K.
Darus, M.
and
Forster-Heinlein, Brigitte
2008.
On Integral Operator Defined by Convolution Involving Hybergeometric Functions.
International Journal of Mathematics and Mathematical Sciences,
Vol. 2008,
Issue. 1,
Wang, Zhi-Gang
Jiang, Yue-Ping
and
Srivastava, H.M.
2009.
Some subclasses of meromorphically multivalent functions associated with the generalized hypergeometric function.
Computers & Mathematics with Applications,
Vol. 57,
Issue. 4,
p.
571.
Haji Mohd, Maisarah
Ali, RosihanM
Keong, LeeSee
and
Ravichandran, V
2009.
Subclasses of Meromorphic Functions Associated with Convolution.
Journal of Inequalities and Applications,
Vol. 2009,
Issue. 1,
p.
190291.
Wang, Zhi-Gang
Xu, Neng
and
Acu, Mugur
2010.
Certain subclasses of multivalent analytic functions defined by multiplier transforms.
Applied Mathematics and Computation,
Vol. 216,
Issue. 1,
p.
192.
Aouf, M.K.
and
EL-Ashwash, R.M.
2010.
Some applications of differential subordination on analytic functions.
Complex Variables and Elliptic Equations,
Vol. 55,
Issue. 11,
p.
1059.
Ali, RosihanM
Mahnaz, MoradiNargesi
Ravichandran, V
and
Subramanian, KG
2010.
Convolution Properties of Classes of Analytic and Meromorphic Functions.
Journal of Inequalities and Applications,
Vol. 2010,
Issue. 1,
p.
385728.
Lee, S.K.
and
Khairnar, S.M.
2011.
A NEW SUBCLASS OF ANALYTIC FUNCTIONS DEFINED BY CONVOLUTION.
Korean Journal of Mathematics,
Vol. 19,
Issue. 4,
p.
351.
Srivastava, H.M.
Khairnar, S.M.
and
More, Meena
2011.
Inclusion properties of a subclass of analytic functions defined by an integral operator involving the Gauss hypergeometric function.
Applied Mathematics and Computation,
Vol. 218,
Issue. 7,
p.
3810.
Abubaker, Afaf A. Ali
Darus, Maslina
and
Kanas, Stanisława R.
2011.
On Starlike and Convex Functions with Respect to k‐Symmetric Points.
International Journal of Mathematics and Mathematical Sciences,
Vol. 2011,
Issue. 1,
Sim, Young Jae
and
Kwon, Oh Sang
2012.
A Subclass of Meromorphic Close-to-Convex Functions of Janowski's Type.
International Journal of Mathematics and Mathematical Sciences,
Vol. 2012,
Issue. ,
p.
1.
Aouf, M. K.
Shamandy, A.
El-Ashwah, R. M.
and
Ali, E. E.
2012.
SOME SUBCLASSES OF MEROMORPHICALLY MULTIVALENT FUNCTIONS ASSOCIATED WITH THE GENERALIZED MULTIPLIER TRANSFORMATIONS.
Asian-European Journal of Mathematics,
Vol. 05,
Issue. 01,
p.
1250001.
El-Ashwash, Rabha M.
Aouf, Mohamed K.
and
Darus, Maslina
2013.
DIFFERENTIAL SUBORDINATION RESULTS FOR ANALYTIC FUNCTIONS.
Asian-European Journal of Mathematics,
Vol. 06,
Issue. 04,
p.
1350044.
Xu, Qing-Hua
Xiao, Hai-Gen
and
Srivastava, H.M.
2014.
Some applications of differential subordination and the Dziok–Srivastava convolution operator.
Applied Mathematics and Computation,
Vol. 230,
Issue. ,
p.
496.
Ali, E. E.
2017.
Some Subclasses of Meromorphically Functions Associated with the Convolution Structure.
Annals of West University of Timisoara - Mathematics and Computer Science,
Vol. 55,
Issue. 1,
p.
3.
Gandhi, Shweta
and
Ravichandran, V.
2017.
Starlike functions associated with a lune.
Asian-European Journal of Mathematics,
Vol. 10,
Issue. 04,
p.
1750064.
Ghanim, F
2018.
A new study of generalized Ma-Minda type class of meromorphic functions.
Journal of Physics: Conference Series,
Vol. 1132,
Issue. ,
p.
012011.


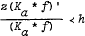 , where
, where 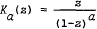 (a real),
(a real), 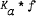 denotes the Hadamard product of
denotes the Hadamard product of 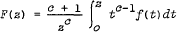 . It is proved that
. It is proved that 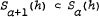 for
for 