No CrossRef data available.
Article contents
SOLUTIONS TO A LEBESGUE–NAGELL EQUATION
Part of:
Diophantine equations
Published online by Cambridge University Press: 24 May 2021
Abstract
We find all integer solutions to the equation
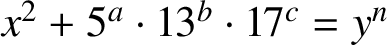$x^2+5^a\cdot 13^b\cdot 17^c=y^n$
with
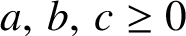$a,\,b,\,c\geq 0$
,
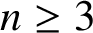$n\geq 3$
,
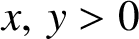$x,\,y>0$
and
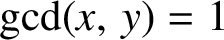$\gcd (x,\,y)=1$
. Our proof uses a deep result about primitive divisors of Lucas sequences in combination with elementary number theory and computer search.
MSC classification
Primary:
11D61: Exponential equations
Secondary:
11D72: Equations in many variables
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 105 , Issue 1 , February 2022 , pp. 19 - 30
- Copyright
- © 2021 Australian Mathematical Publishing Association Inc.
Footnotes
The author is partially supported by the Vietnam Institute for Advanced Study in Mathematics (VIASM) and the Vietnam National Foundation for Science and Technology Development (NAFOSTED) (grant number 101.04-2019.314).
References
Alan, M. and Zengin, U., ‘On the Diophantine equation
${x}^2+{3}^a\cdot 4{1}^b={y}^n$
’, Period. Math. Hungar. 81 (2020), 284–291.CrossRefGoogle Scholar
${x}^2+{3}^a\cdot 4{1}^b={y}^n$
’, Period. Math. Hungar. 81 (2020), 284–291.CrossRefGoogle ScholarArif, S. A. and Muriefah, F. S. A., ‘On the Diophantine equation
${x}^2+{q}^{2k+1}={y}^n$
’, J. Number Theory 95 (2002), 95–100.CrossRefGoogle Scholar
${x}^2+{q}^{2k+1}={y}^n$
’, J. Number Theory 95 (2002), 95–100.CrossRefGoogle ScholarBérczes, A. and Pink, I., ‘On the Diophantine equation
${x}^2+{p}^{2k}={y}^n$
’, Arch. Math. 91 (2008), 505–517.CrossRefGoogle Scholar
${x}^2+{p}^{2k}={y}^n$
’, Arch. Math. 91 (2008), 505–517.CrossRefGoogle ScholarBérczes, A. and Pink, I., ‘On the Diophantine equation
${x}^2+{d}^{2l+1}={y}^n$
’, Glasg. Math. J. 54 (2012), 415–428.CrossRefGoogle Scholar
${x}^2+{d}^{2l+1}={y}^n$
’, Glasg. Math. J. 54 (2012), 415–428.CrossRefGoogle ScholarBilu, Y., Hanrot, G. and Voutier, P. M., ‘Existence of primitive divisors of Lucas and Lehmer numbers. With an appendix by M. Mignotte’, J. reine angew. Math. 539 (2001), 75–122.Google Scholar
Bosma, W., Cannon, J. and Playoust, C., ‘The Magma algebra system. I. The user language’, J. Symbolic Comput. 24(3–4) (1997), 235–265.CrossRefGoogle Scholar
Bugeaud, Y., Mignotte, M. and Siksek, S., ‘Classical and modular approaches to exponential Diophantine equations II: The Lebesgue–Nagell equation’, Compos. Math. 142 (2006), 31–62.CrossRefGoogle Scholar
Cangül, I. N., Demirci, M., Inam, I., Luca, F. and Soydan, G., ‘On the Diophantine equation
${x}^2+{2}^a\cdot {3}^b\cdot 1{1}^c={y}^n$
’, Math. Slovaca 63(3) (2013), 647–659.CrossRefGoogle Scholar
${x}^2+{2}^a\cdot {3}^b\cdot 1{1}^c={y}^n$
’, Math. Slovaca 63(3) (2013), 647–659.CrossRefGoogle ScholarChakraborty, K., Hoque, A. and Sharma, R., ‘On the solutions of certain Lebesgue– Ramanujan–Nagell equations’, Rocky Mountain J. Math., to appear.Google Scholar
Cohn, J. H. E., ‘The Diophantine equation
${x}^2+C={y}^n$
’, Acta. Arith. 65 (1993), 367–381.CrossRefGoogle Scholar
${x}^2+C={y}^n$
’, Acta. Arith. 65 (1993), 367–381.CrossRefGoogle ScholarGodinho, H., Marques, D. and Togbé, A., ‘On the Diophantine equation
${x}^2+C={y}^n$
for
$C={2}^a\cdot {3}^b\cdot 1{7}^c$
and
$C={2}^a\cdot 1{3}^b\cdot 1{7}^c$
’, Math. Slovaca 66 (3) (2016), 565–574.CrossRefGoogle Scholar
${x}^2+C={y}^n$
for
$C={2}^a\cdot {3}^b\cdot 1{7}^c$
and
$C={2}^a\cdot 1{3}^b\cdot 1{7}^c$
’, Math. Slovaca 66 (3) (2016), 565–574.CrossRefGoogle ScholarGoins, E., Luca, F. and Togbé, A., ‘On the Diophantine equation
${x}^2+{2}^{\alpha}\cdot {5}^{\beta}\cdot 1{3}^{\gamma }={y}^n$
’, in: Algorithmic Number Theory, 8th International Symposium, ANTS-VIII, Banff, Canada, May 17–22, 2008 (eds. van der Poorten, A. J. and Stein, A.) (Springer, Berlin–Heidelberg, 2008), 430–442.Google Scholar
${x}^2+{2}^{\alpha}\cdot {5}^{\beta}\cdot 1{3}^{\gamma }={y}^n$
’, in: Algorithmic Number Theory, 8th International Symposium, ANTS-VIII, Banff, Canada, May 17–22, 2008 (eds. van der Poorten, A. J. and Stein, A.) (Springer, Berlin–Heidelberg, 2008), 430–442.Google ScholarLe, M. and Soydan, G., ‘A brief survey on the generalized Lebesgue–Ramanujan–Nagell equation’, Surveys in Mathematics and its Applications 15 (2020), 473–523.Google Scholar
Muriefah, F. S. A., Luca, F. and Togbé, A., ‘On the Diophantine equation
${x}^2+{5}^a\cdot 1{3}^b={y}^n$
’, Glasg. Math. J. 50 (2008), 175–181.Google Scholar
${x}^2+{5}^a\cdot 1{3}^b={y}^n$
’, Glasg. Math. J. 50 (2008), 175–181.Google ScholarPink, I., ‘On the Diophantine equation
${x}^2+{2}^a\cdot {3}^b\cdot {5}^c\cdot {7}^d={y}^n$
’, Publ. Math. Debrecen 70(1–2) (2007), 149–166.CrossRefGoogle Scholar
${x}^2+{2}^a\cdot {3}^b\cdot {5}^c\cdot {7}^d={y}^n$
’, Publ. Math. Debrecen 70(1–2) (2007), 149–166.CrossRefGoogle ScholarPink, I. and Rábai, Z., ‘On the Diophantine equation
${x}^2+{5}^k\cdot 1{7}^l={y}^n$
’, Commun. Math. 19 (2011), 1–19.Google Scholar
${x}^2+{5}^k\cdot 1{7}^l={y}^n$
’, Commun. Math. 19 (2011), 1–19.Google ScholarXiaowei, P., ‘The exponential Lebesgue–Nagell equation
${x}^2+{p}^{2m}={y}^n$
’, Period. Math. Hungar. 67(2) (2013), 231–242.CrossRefGoogle Scholar
${x}^2+{p}^{2m}={y}^n$
’, Period. Math. Hungar. 67(2) (2013), 231–242.CrossRefGoogle ScholarZhu, H. L. and Le, M. H., ‘On some generalized Lebesgue–Nagell equations’, J. Number Theory 131 (2011), 458–469.CrossRefGoogle Scholar