Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T14:17:10.107Z Has data issue: false hasContentIssue false
  • English
  • Français

SLANT CURVES IN CONTACT PSEUDO-HERMITIAN 3-MANIFOLDS

Part of: Fairly general properties Global differential geometry

Published online by Cambridge University Press:  01 December 2008

JONG TAEK CHO  and
JI-EUN LEE
JONG TAEK CHO*
Affiliation:
Department of Mathematics, CNU The Institute of Basic Science, Chonnam National University, Gwangju 500–757, Korea (email: [email protected])
JI-EUN LEE
Affiliation:
National Institute for Mathematical Sciences, 385-16 Doryong-dong, Yuseong-gu Daejeon 305-340, Korea (email: [email protected]) Department of Mathematics, Graduate School, Chonnam National University, Gwangju 500–757, Korea (email: [email protected])
*
✉For correspondence; e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

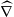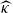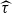By using the pseudo-Hermitian connection (or Tanaka–Webster connection) , we construct the parametric equations of Legendre pseudo-Hermitian circles (whose -geodesic curvature is constant and -geodesic torsion is zero) in S3. In fact, it is realized as a Legendre curve satisfying the -Jacobi equation for the 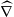-geodesic vector field along it.

Keywords

unit spheresLegendre curvespseudo-Hermitian circles

MSC classification

Secondary: 53C25: Special Riemannian manifolds (Einstein, Sasakian, etc.) 53C43: Differential geometric aspects of harmonic maps 54D10: Lower separation axioms ($T_0$--$T_3$, etc.)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 78 , Issue 3 , December 2008 , pp. 383 - 396
Copyright
Copyright © 2009 Australian Mathematical Society

Footnotes

The second author was supported by the Korea Research Council of Fundamental Science & Technology (KRCF), Grant No. C-RESEARCH-2006-11-NIMS.

References

[1]Belkhelfa, M., Dillen, F. and Inoguchi, J., ‘Surfaces with parallel second fundamental form in Binachi–Cartan–Vranceanu spaces’, in: PDE’s, Submanifolds and Affine Differential Geometry (Warsaw, 2000), Banach Center Publications, 57 (Polish Academy of Science, Warsaw, 2002), pp. 67–87.Google Scholar
[2]Bianchi, L., Lezioni di Geometrie Differenziale (E. Spoerri Librao-Editore, 1894).Google Scholar
[3]Blair, D. E., Riemannian Geometry of Contact and Symplectic Manifolds, Progress in Mathematics, 203 (Birkhäuser, Boston, MA, 2002).CrossRefGoogle Scholar
[4]Caddeo, R., Montaldo, S. and Oniciuc, C., ‘Biharmonic submanifolds of S 3’, Internat. J. Math. 12 (2001), 867–876.Google Scholar
[5]Caddeo, R., Montaldo, S. and Piu, P., ‘Biharmonic maps’, Contemp. Math. 288 (2001), 286–290.Google Scholar
[6]Cartan, E., Leçons sur la géométrie des espaces de Riemann, 2nd edn (Gauthier-Villards, Paris, 1946).Google Scholar
[7]Chen, B. Y. and Ishikawa, S., ‘Biharmonic surfaces in pseudo-Euclidean spaces’, Mem. Fac. Kyushu Univ. Ser. A 45(2) (1991), 323–347.Google Scholar
[8]Cho, J. T., ‘Geometry of contact strongly pseudo-convex CR-maniflods’, J. Korean Math. Soc. 43(5) (2006), 1019–1045.CrossRefGoogle Scholar
[9]Cho, J. T., Inoguchi, J. and Lee, J.-E., ‘On slant curves in Sasakian 3-manifolds’, Bull. Austral. Math. Soc. 74(3) (2006), 359–367.Google Scholar
[10]Cho, J. T., Inoguchi, J. and Lee, J.-E., ‘Biharmonic curves in 3-dimensional Sasakian space form’, Ann. Mat. Pura Appl. 186 (2007), 685–701.Google Scholar
[11]Inoguchi, J., ‘Submanifolds with harmonic mean curvature in contact 3-manifold’, Colloq. Math. 100(6) (2004), 163–179.Google Scholar
[12]Kobayashi, S., Transformation Groups in Differential Geometry, Ergebnisse der Mathematik und Ihere Grenzgebiete, 70 (Springer, Berlin, 1972).Google Scholar
[13]Tamura, M., ‘Gauss maps of surfaces in contact space forms’, Comment. Math. Univ. St. Pauli 52 (2003), 117–123.Google Scholar
[14]Tanaka, N., ‘On non-degenerate real hypersurfaces, graded Lie algebras and Cartan connections’, Japan J. Math. 2 (1976), 131–190.Google Scholar
[15]Tanno, S., ‘Variantional problems on contact Riemannian manifolds’, Trans. Amer. Math.Soc. 314 (1989), 349–379.Google Scholar
[16]Vranceanu, G., Leçons de géométrie différentielle, Éditions de l’Académie de la République Populaire Roumaine, Bucharest (1947).Google Scholar
[17]Webster, S. M., ‘Pseudohermitian structures on a real hypersurface’, J. Differential Geom. 13 (1978), 25–41.Google Scholar