Article contents
The skeleton of a variety of groups
Published online by Cambridge University Press: 17 April 2009
Abstract
The skeleton 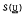 of a variety
of a variety 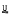 of groups is defined to be the intersection of the section closed classes of groups which generate
of groups is defined to be the intersection of the section closed classes of groups which generate 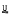 . If m is an integer, m > 1,
. If m is an integer, m > 1, 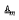 is the variety of all abelian groups of exponent dividing m, and
is the variety of all abelian groups of exponent dividing m, and 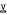 , is any locally finite variety, it is shown that the skeleton of the product variety
, is any locally finite variety, it is shown that the skeleton of the product variety 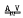 is the section closure of the class of finite monolithic groups in
is the section closure of the class of finite monolithic groups in 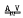 . In particular, S
. In particular, S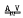 ) generates
) generates 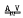 . The elements of S
. The elements of S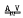 are described more explicitly and as a consequence it is shown that S
are described more explicitly and as a consequence it is shown that S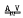 consists of all finite groups in
consists of all finite groups in 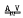 if and only if m is a power of some prime p and the centre of the countably infinite relatively free group of
if and only if m is a power of some prime p and the centre of the countably infinite relatively free group of 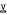 , is a p–group.
, is a p–group.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1972
References
- 6
- Cited by


