Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ma, Ruyun
Luo, Hua
and
Gao, Chenghua
2008.
On Nonresonance Problems of Second-Order Difference Systems.
Advances in Difference Equations,
Vol. 2008,
Issue. 1,
p.
469815.


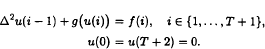 We establish the relationship between the number of sign-variation of
We establish the relationship between the number of sign-variation of 