Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-28T17:02:25.805Z Has data issue: false hasContentIssue false
  • English
  • Français

SHIFTED CONVOLUTION SUM OF 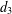$d_{3}$ AND THE FOURIER COEFFICIENT OF HECKE–MAASS FORMS

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  02 June 2015

HENGCAI TANG
HENGCAI TANG*
Affiliation:
School of Mathematics and Information Sciences, Institute of Modern Mathematics, Henan University, Kaifeng, Henan 475004, PR China email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 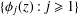$\{{\it\phi}_{j}(z):j\geq 1\}$ be an orthonormal basis of Hecke–Maass cusp forms with Laplace eigenvalue 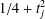$1/4+t_{j}^{2}$. Let 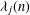${\it\lambda}_{j}(n)$ be the $n$th Fourier coefficient of ${\it\phi}_{j}$ and 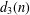$d_{3}(n)$ the divisor function of order three. In this paper, by the circle method and the Voronoi summation formula, the average value of the shifted convolution sum for 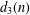$d_{3}(n)$ and 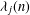${\it\lambda}_{j}(n)$ is considered, leading to the estimate

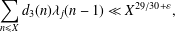$$\begin{eqnarray}\displaystyle \mathop{\sum }_{n\leq X}d_{3}(n){\it\lambda}_{j}(n-1)\ll X^{29/30+{\it\varepsilon}}, & & \displaystyle \nonumber\end{eqnarray}$$
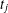where the implied constant depends only on $t_{j}$ and ${\it\varepsilon}$.

Keywords

divisor functionHecke–Maass formVoronoi summation formula

MSC classification

Primary: 11F30: Fourier coefficients of automorphic forms
Secondary: 11F11: Holomorphic modular forms of integral weight 11F66: Langlands $L$-functions; one variable Dirichlet series and functional equations
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 92 , Issue 2 , October 2015 , pp. 195 - 204
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Adolphson, A. and Sperber, S., ‘Exponential sums and Newton polyhedra, cohomology and estimates’, Ann. of Math. (2) 130 (1989), 367–406.CrossRefGoogle Scholar
Ivić, A., ‘On the ternary additive divisor problem and the sixth moment of the zeta-function’, in: Sieve Methods, Exponential Sums, and their Applications in Number Theory, LMS Lecture Note Series, 237 (Cambridge University Press, Cambridge, 1997), 205–243.CrossRefGoogle Scholar
Jutila, M., ‘Transformations of exponential sums’, in: Proc. Amalfi Conf. Analytic Number Theory, Maiori 1989 (University of Salerno, Salerno, 1992), 263–270.Google Scholar
Kim, H. H. and Sarnak, P., ‘Appendix 2: refined estimates towards the Ramanujan and Selberg conjectures’, J. Amer. Math. Soc. 16 (2003), 175–181.Google Scholar
Kowalski, E., Michel, P. and Vanderkam, J., ‘Rankin–Selberg L-functions in the level aspect’, Duke Math. J. 114 (2002), 123–191.CrossRefGoogle Scholar
Munshi, R., ‘Shifted convolution of divisor function d 3 and Ramanujan 𝜏-function’, in: The Legacy of Srinivasa Ramanujan, Lecture Note Series, 20 (Ramanujan Mathematical Society, India, 2013), 251–260.Google Scholar
Munshi, R., ‘Shifted convolution sums for GL (3) × GL (2)’, Duke Math. J. 162 (2013), 2345–2362.CrossRefGoogle Scholar
Pitt, N. J. E., ‘On shifted convolutions of 𝜁3(s) with automorphic L-functions’, Duke Math. J. 77 (1995), 383–406.CrossRefGoogle Scholar
Pitt, N. J. E., ‘On cusp form coefficients in exponential sums’, Q. J. Math. 52 (2001), 485–497.CrossRefGoogle Scholar