No CrossRef data available.
Article contents
Set covering number for a finite set
Published online by Cambridge University Press: 17 April 2009
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Given a finite set S of cardinality N, the minimum number of j-subsets of S needed to cover all the r-subsets of S is called the covering number C(N, j, r). While Erdös and Hanani's conjecture that 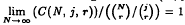 was proved by Rödl, no nontrivial upper bound for C(N, j, r) was known for finite N. In this note we obtain a nontrivial upper bound by showing that for finite N,
was proved by Rödl, no nontrivial upper bound for C(N, j, r) was known for finite N. In this note we obtain a nontrivial upper bound by showing that for finite N, 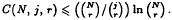
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1996
References
[1]Erdös, P. and Hanani, H., ‘On a limit theorem in combinatorial analysis’, publ. Math. Debrecen 10 (1963), 10–13.CrossRefGoogle Scholar


