Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T07:27:11.201Z Has data issue: false hasContentIssue false
  • English
  • Français

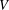A SCHWARZ LEMMA FOR $V$-HARMONIC MAPS AND THEIR APPLICATIONS

Part of: Geometric function theory Holomorphic mappings and correspondences Complex manifolds Variational problems in infinite-dimensional spaces

Published online by Cambridge University Press:  17 August 2017

QUN CHEN  and
GUANGWEN ZHAO
QUN CHEN*
Affiliation:
School of Mathematics and Statistics, Wuhan University, Wuhan 430072, PR China email [email protected]
GUANGWEN ZHAO
Affiliation:
School of Mathematics and Statistics, Wuhan University, Wuhan 430072, PR China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

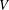We establish a Schwarz lemma for $V$-harmonic maps of generalised dilatation between Riemannian manifolds. We apply the result to obtain corresponding results for Weyl harmonic maps of generalised dilatation from conformal Weyl manifolds to Riemannian manifolds and holomorphic maps from almost Hermitian manifolds to quasi-Kähler and almost Kähler manifolds.

Keywords

Schwarz lemmaV-harmonic mapOmori–Yau maximum principleholomorphic mapalmost Hermitian manifold

MSC classification

Primary: 58E20: Harmonic maps , etc.
Secondary: 30C80: Maximum principle; Schwarz's lemma, Lindelöf principle, analogues and generalizations; subordination 32Q60: Almost complex manifolds 32H02: Holomorphic mappings, (holomorphic) embeddings and related questions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 96 , Issue 3 , December 2017 , pp. 504 - 512
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

Footnotes

This work is partially supported by the NSF China (Grant number 11571259).

References

Ahlfors, L. V., ‘An extension of Schwarz’s lemma’, Trans. Amer. Math. Soc. 43(3) (1938), 359–364.Google Scholar
Chen, Q., Jost, J. and Wang, G., ‘A maximum principle for generalizations of harmonic maps in Hermitian, Affine, Weyl, and Finsler geometry’, J. Geom. Anal. 25(4) (2015), 2407–2426.CrossRefGoogle Scholar
Chen, Q. and Qiu, H., ‘Rigidity of self-shrinkers and translating solitons of mean curvature flows’, Adv. Math. 294 (2016), 517–531.Google Scholar
Chern, S.-S., ‘On holomorphic mappings of Hermitian manifolds of the same dimension’, in: Proc. Sympos. Pure Math., Vol. 11 (Amer. Math. Soc., Providence, RI, 1968), 157–170.Google Scholar
Goldberg, S. I. and Har’El, Z., ‘A general Schwarz lemma for Riemannian-manifolds’, Bull. Greek Math. Soc. 18(1) (1977), 141–148.Google Scholar
Goldberg, S. I., Ishihara, T. and Petridis, N. C., ‘Mappings of bounded dilatation of Riemannian manifolds’, J. Differ. Geom. 10(4) (1975), 619–630.Google Scholar
Gray, A., ‘Minimal varieties and almost Hermitian submanifolds’, Michigan Math. J. 12(3) (1965), 273–287.CrossRefGoogle Scholar
Har’El, Z. and Goldberg, S. I., ‘Mappings of almost Hermitian manifolds’, J. Differ. Geom. 14(1) (1979), 67–80.Google Scholar
Kokarev, G., ‘On pseudo-harmonic maps in conformal geometry’, Proc. London Math. Soc. 99(1) (2009), 168–194.Google Scholar
Lu, Y.-C., ‘Holomorphic mappings of complex manifolds’, J. Differ. Geom. 2(3) (1968), 299–312.Google Scholar
Shen, C., ‘A generalization of the Schwarz–Ahlfors lemma to the theory of harmonic maps’, J. reine angew. Math. 348 (1984), 23–33.Google Scholar
Tosatti, V., ‘A general Schwarz lemma for almost-Hermitian manifolds’, Comm. Anal. Geom. 15(5) (2007), 1063–1086.Google Scholar
Xin, Y., Geometry of Harmonic Maps (Birkhäser, Boston, 1996).Google Scholar
Yang, H. and Chen, Z., ‘On the Schwarz lemma for complete Hermitian manifolds’, in: Several Complex Variables (Springer, 1984), 99–116.Google Scholar
Yau, S.-T., ‘A general Schwarz lemma for Kahler manifolds’, Amer. J. Math. 100(1) (1978), 197–203.Google Scholar