A RIGIDITY PROPERTY OF PLURIHARMONIC MAPS FROM PROJECTIVE MANIFOLDS

Abstract

Suppose M is a complex projective manifold of dimension 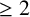$\geq 2$, V is the support of an ample divisor in M and U is an open set in M that intersects each irreducible component of V. We show that a pluriharmonic map 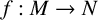$f:M\to N$ into a Kähler manifold N is holomorphic whenever $f\vert _{V\,\cap \, U}$ is holomorphic.

Sampson [4] proved a unique continuation theorem for harmonic mappings of Riemannian manifolds. Siu [5] showed that a harmonic mapping of connected Kähler manifolds $f: M\to N$ is holomorphic whenever $f\vert _U$ is holomorphic for some nonempty open set $U\subset M$ . It is not difficult to see that, in general, U cannot be replaced by an analytic hypersurface $V\subset M$ . For example, take $f= \phi \times \psi $ , where $\phi : X\to Y$ is a holomorphic mapping of connected Kähler manifolds and $\psi :S\to Y$ is a harmonic map from a Riemann surface S. If $\psi $ is not holomorphic, then f is not holomorphic, but $f\vert _{X\times \{p\}}$ is holomorphic for every $p\in S$ .

Siu’s unique continuation theorem is a basic ingredient in the proof of the strong rigidity theorem for compact Kähler manifolds [5, Theorem 2]. Suppose $M\subset \mathbb {P}^k$ is a projective manifold of dimension $\geq 2$ and V is a smooth hyperplane section of M. We shall see that if $f:M\to N$ is a pluriharmonic map into a Kähler manifold N such that $f\vert _V$ is holomorphic, then f is holomorphic. This result is motivated by the application of Toledo’s theorem on plurisubharmonicity of the energy to rigidity theory [2, 6]. Note that we may weaken the assumption that $f\vert _V$ is holomorphic by applying Siu’s unique continuation theorem.

The main purpose of this note is to establish the following result.

Proposition 1. Suppose $f:M\to N$ is a pluriharmonic map from a projective manifold M into a Kähler manifold N, with ${dim}\, M \geq 2$ . Suppose $D=\sum _{i=1}^k a_i V_i$ is an ample divisor in M, where $a_i\in \mathbb {Z}$ , $a_i\neq 0$ , and $V_i$ is an irreducible hypersurface in M, for $i=1,\ldots ,k$ . Let V be the support of D and let U be an open set in M such that $V_i\hspace {0.02cm}\cap \hspace {0.02cm} U\neq \emptyset $ for each i. If $f\vert _{V\,\cap \, U}$ is holomorphic, then f is holomorphic.

Remark 2. Proposition 1 generalises the following result due to Gromov [2, Section 4.6] (see also [6, Theorem 5]). Suppose $f:M\to N$ is a pluriharmonic map from a smooth projective surface M into a quotient $N=\Omega \,/\,\Gamma $ of an irreducible bounded symmetric domain $\Omega $ . If $f\vert _V$ is holomorphic for some general element V of a Lefschetz pencil on M, then f is holomorphic.

Proof of Proposition 1.

Let $\omega $ be a Kähler form on M representing the first Chern class $c_1(\mathcal {O}(D))$ associated to D and let $\omega _N = \sqrt {-1}\, h_{\alpha \overline {\beta }} \,dw^\alpha \wedge d \overline {w^\beta }$ denote the Kähler form on N. If $\phi :X\to N$ is a smooth map from an n-dimensional complex submanifold $X\subset M$ into N, we let $\omega _X=\omega \vert _X$ and $\varepsilon "(\phi )= \sqrt {-1}\, h_{\alpha \overline {\beta }} \,\partial \overline {\phi ^\beta }\wedge \overline {\partial } \phi ^\alpha $ , which are real $(1,1)$ -forms on X such that

$$ \begin{align*} \varepsilon"(\phi)\wedge \omega_X^{n-1}/(n-1)! =\vert\overline{\partial}\phi\vert^2\,\omega_X^n/n!\quad \text{if}\ n\geq 1,\end{align*} $$

and we define $E"(\phi )=\int _X\,\vert \overline {\partial }\phi \vert ^2\,dV_{\omega _X}$ provided that the integral is finite.

Since $c_1(\mathcal {O}(D))=[\omega ]$ is the Poincaré dual of the fundamental homology class $[D]$ of D,

(1) $$ \begin{align} E"(f)=\int_M\, \varepsilon"({f})\wedge\frac{\omega^{m-1}}{(m-1)!}=\sum_{i=1}^k\,a_i\cdot\int_{D_i}\,\hspace{-0.02cm} \varepsilon"(f\vert_{D_i})\wedge\frac{\omega_{D_i}^{m-2}}{(m-2)!}=\sum_{i=1}^k a_i E"(f\vert_{D_i}), \end{align} $$

where $m=\text {dim}\, M$ and $D_i$ is the smooth locus of $V_i$ for $1\leq i\leq k$ . Note that $\varepsilon "(f\vert _{D_i})= \varepsilon "(f)\vert _{D_i}$ for each i, and that $\varepsilon "(f)$ is closed because f is pluriharmonic [3, Lemma 3.10]. Since $f\vert _{V\,\cap \, U}$ is holomorphic, $f\vert _{D_i}$ is holomorphic for each i (see [5, pages 88–89]) and we conclude from (1) that f is holomorphic.

We shall see that the analogue of (1) holds for the Dirichlet energy $E(f)$ . Suppose that $f: M\to N$ is a pluriharmonic map from a projective manifold M of dimension $m\geq 2$ into a Riemannian manifold $(N, h=h_{ij}\,dy^i\otimes dy^{\,j})$ . We fix a Kähler form $\omega $ on M with integral cohomology class and choose a divisor $D=\sum _{i=1}^k a_i V_i$ such that $c_1(\mathcal {O}(D))=[\omega ]$ , where $a_i$ is a nonzero integer and $V_i$ is an irreducible hypersurface in M with smooth locus $D_i$ for each i.

Recall that if $\phi :X\to N$ is a smooth map from a Kähler submanifold $X\subset M$ , with Kähler form $\omega _X=\omega \vert _X$ , then the energy density $e(\phi )$ of $\phi $ is given by $e(\phi ) = \tfrac 12\vert {d}\phi \vert ^2=\langle \varepsilon (\phi ), \omega _X\rangle $ , where $\varepsilon (\phi )=\sqrt {-1}\,h_{ij}\,\partial \phi ^i\wedge \overline {\partial }\phi ^{\,j}$ is a real (1,1)-form on X, and the energy $E(\phi )$ of $\phi $ is given by $E(\phi )=\int _X e(\phi )\,d V_{\omega _X}$ .

Since f is pluriharmonic, the $(1,1)$ -form $\varepsilon (f)$ is closed (see, for example, [3, Lemma 2.2]). For $i=1,\ldots ,k$ , $\varepsilon (f)\vert _{D_i}= \varepsilon (f\vert _{D_i})$ . Since $c_1(\mathcal {O}(D))=[\omega ]$ is the Poincaré dual of $[D]$ , it follows that

(2) $$ \begin{align} E(f)=\int_M\, \varepsilon({f})\wedge\frac{\omega^{m-1}}{(m-1)!}=\sum_{i=1}^k\,a_i\cdot\int_{D_i}\,\hspace{-0.02cm} \varepsilon(f\vert_{D_i})\wedge\frac{\omega_{D_i}^{m-2}}{(m-2)!}=\sum_{i=1}^k a_i E(f\vert_{D_i}). \end{align} $$

Example 3. Suppose S is a compact Riemann surface of genus $g\geq 2$ . The Jacobian $J(S)$ of S is an Abelian variety with a principal polarisation $[\omega ]=c_1(\mathcal {O}(\Theta ))$ , where $\Theta $ is a theta divisor in $J(S)$ , that is, a translate of the zero locus of the Riemann theta function. Put $M=J(S)$ and let $f: M\to N$ be a pluriharmonic map into a Kähler manifold N. Then Proposition 1 shows that if $f\vert _G$ is holomorphic for some nonempty open subset G of $\Theta $ , then f is holomorphic.

Let $W=\mu (S)$ be the image of S under the Abel–Jacobi map $\mu : S\to J(S)$ . We have

$$ \begin{align*}E"(f)=\int_M\, \varepsilon"({f})\wedge\frac{\omega^{g-1}}{(g-1)!}=\int_{W}\,\hspace{-0.02cm} \varepsilon"(f\vert_{W})= E"(f\vert_{W}), \end{align*} $$

since $[({1}/{(g-1)!})\,\omega ^{g-1}]$ is the Poincaré dual of $[W]$ (see, for example, [1, page 350]). Similarly, $E(f)=E(f\vert _W)$ . Using (1) and (2), we conclude that

$$ \begin{align*}E"(f)=E"(f\vert_{\Theta^*})=E"(f\vert_W)\quad \text{and}\quad E(f)=E(f\vert_{\Theta^*})=E(f\vert_W),\end{align*} $$

where $\Theta ^*$ denotes the smooth locus of $\Theta $ . As in the proof of Proposition 1, it follows that if $f\vert _G$ is holomorphic for some nonempty open subset G of W, then f is holomorphic.