Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Poor, Cris
and
Yuen, David S.
2003.
Slopes of integral lattices.
Journal of Number Theory,
Vol. 100,
Issue. 2,
p.
363.
Poor, C.
and
Yuen, D. S.
2007.
Dimensions of cusp forms for Γ0(p) in degree two and small weights.
Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg,
Vol. 77,
Issue. 1,
p.
59.
POOR, Cris
and
YUEN, David S.
2007.
Computations of spaces of Siegel modular cusp forms.
Journal of the Mathematical Society of Japan,
Vol. 59,
Issue. 1,
OURA, MANABU
POOR, CRIS
and
YUEN, DAVID S.
2008.
TOWARDS THE SIEGEL RING IN GENUS FOUR.
International Journal of Number Theory,
Vol. 04,
Issue. 04,
p.
563.
Poor, Cris
Schmidt, Ralf
and
Yuen, David S.
2018.
Paramodular forms of level 8 and weights 10 and 12.
International Journal of Number Theory,
Vol. 14,
Issue. 02,
p.
417.


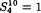 .
.