Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T04:15:34.716Z Has data issue: false hasContentIssue false
  • English
  • Français

RESOLVABLE MENDELSOHN DESIGNS AND FINITE FROBENIUS GROUPS

Part of: Designs and configurations

Published online by Cambridge University Press:  30 May 2018

D. F. HSU  and
SANMING ZHOU Open the ORCID record for SANMING ZHOU [Opens in a new window]
D. F. HSU
Affiliation:
Department of Computer and Information Sciences, Fordham University, New York, NY 10023, USA email [email protected]
SANMING ZHOU*
Affiliation:
School of Mathematics and Statistics, The University of Melbourne, Parkville, VIC 3010, Australia email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove the existence and give constructions of a 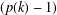$(p(k)-1)$-fold perfect resolvable 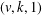$(v,k,1)$-Mendelsohn design for any integers 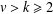$v>k\geq 2$ with 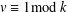$v\equiv 1\hspace{0.2em}{\rm mod}\hspace{0.2em}\,k$ such that there exists a finite Frobenius group whose kernel 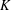$K$ has order $v$ and whose complement contains an element 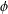$\unicode[STIX]{x1D719}$ of order 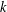$k$, where 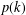$p(k)$ is the least prime factor of 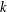$k$. Such a design admits 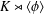$K\rtimes \langle \unicode[STIX]{x1D719}\rangle$ as a group of automorphisms and is perfect when 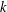$k$ is a prime. As an application we prove that for any integer 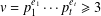$v=p_{1}^{e_{1}}\cdots p_{t}^{e_{t}}\geq 3$ in prime factorisation and any prime 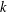$k$ dividing 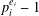$p_{i}^{e_{i}}-1$ for 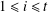$1\leq i\leq t$, there exists a resolvable perfect 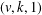$(v,k,1)$-Mendelsohn design that admits a Frobenius group as a group of automorphisms. We also prove that, if 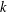$k$ is even and divides 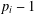$p_{i}-1$ for 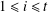$1\leq i\leq t$, then there are at least 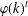$\unicode[STIX]{x1D711}(k)^{t}$ resolvable 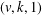$(v,k,1)$-Mendelsohn designs that admit a Frobenius group as a group of automorphisms, where $\unicode[STIX]{x1D711}$ is Euler’s totient function.

Keywords

Mendelsohn designbalanced directed cycle designresolvable Mendelsohn designperfect Mendelsohn designFrobenius groupfixed-point-free automorphism

MSC classification

Primary: 05B05: Block designs
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 98 , Issue 1 , August 2018 , pp. 1 - 13
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

The second author was supported by a Future Fellowship (FT110100629) of the Australian Research Council.

References

Abel, R. J. R. and Bennett, F. E., ‘The existence of (v, 6, 𝜆)-perfect Mendelsohn designs with 𝜆 > 1’, Des. Codes Cryptogr. 40 (2006), 211–224.CrossRefGoogle Scholar
Abel, R. J. R., Bennett, F. E. and Ge, G., ‘Almost resolvable perfect Mendelsohn designs with block size five’, Discrete Appl. Math. 116 (2002), 1–15.CrossRefGoogle Scholar
Abel, R. J. R., Bennett, F. E. and Ge, G., ‘Resolvable perfect Mendelsohn designs with block size five’, Discrete Math. 247(1–3) (2002), 1–12.Google Scholar
Abel, R. J. R., Bennett, F. E. and Zhang, H., ‘Perfect Mendelsohn designs with block size six’, J. Stat. Plan. Inference 86 (2000), 287–319.CrossRefGoogle Scholar
Bennett, F. E., ‘Direct constructions for perfect 3-cyclic designs’, Ann. Discrete Math. 15 (1982), 63–68.Google Scholar
Bennett, F. E., ‘Recent progress on the existence of perfect Mendelsohn designs’, J. Stat. Plan. Inference 94 (2001), 121–138.Google Scholar
Bennett, F. E., Mendelsohn, E. and Mendelsohn, N. S., ‘Resolvable perfect cyclic designs’, J. Combin. Theory Ser. A 29 (1980), 142–150.Google Scholar
Bennett, F. E. and Sotteau, D., ‘Almost resolvable decomposition of K n ∗ ’, J. Combin. Theory Ser. B 30(2) (1981), 228–232.Google Scholar
Bennett, F. E. and Zhang, X., ‘Resolvable Mendelsohn designs with block size 4’, Aequationes Math. 40(2–3) (1990), 248–260.Google Scholar
Bermond, J.-C., Germa, A. and Sotteau, D., ‘Resolvable decomposition of K n ∗ ’, J. Combin. Theory Ser. A 26(2) (1979), 179–185.Google Scholar
Bermond, J.-C. and Sotteau, D., ‘Graph decompositions and G-designs’, in: Proc. 5th British Combin. Conf. (Univ. Aberdeen, Aberdeen, 1975), Congressus Numerantium, XV (Utilitas Math., Winnipeg, Man., 1976), 53–72.Google Scholar
Boykett, T., ‘Construction of Ferrero pairs of all possible orders’, SIAM J. Discrete Math. 14(3) (2001), 283–285.Google Scholar
Brand, N. and Huffman, W. C., ‘Mendelsohn designs admitting the affine group’, Graphs Combin. 3 (1987), 313–324.Google Scholar
Dixon, J. D. and Mortimer, B., Permutation Groups (Springer, New York, 1996).Google Scholar
Evans, A. B., ‘The admissibility of sporadic simple groups’, J. Algebra 321 (2009), 1407–1428.Google Scholar
Evans, A. B., ‘The existence of strong complete mappings of finite groups: A survey’, Discrete Math. 313(11) (2013), 1191–1196.Google Scholar
Friedlander, R. J., Gordon, B. and Tannenbaum, P., ‘Partitions of groups and complete mappings’, Pacific J. Math. 92(2) (1981), 283–293.Google Scholar
Gorenstein, D., Finite Groups, 2nd edn (Chelsea, New York, 1980).Google Scholar
Hall, M. and Paige, L. J., ‘Complete mappings of finite groups’, Pacific J. Math. 5 (1955), 541–549.Google Scholar
Hsu, D. F. and Keedwell, A. D., ‘Generalized complete mappings, neofields, sequenceable groups and block designs I’, Pacific J. Math. 111 (1984), 317–332.Google Scholar
Hsu, D. F. and Keedwell, A. D., ‘Generalized complete mappings, neofields, sequenceable groups and block designs II’, Pacific J. Math. 117 (1985), 291–312.Google Scholar
Mann, H. B., ‘The construction of orthogonal latin squares’, Ann. Math. Statist. 12 (1942), 418–423.CrossRefGoogle Scholar
Mendelsohn, N. S., ‘A natural generalization of Steiner triple systems’, in: Computers in Number Theory (Academic Press, New York, 1971), 323–338.Google Scholar
Mendelsohn, N. S., ‘Perfect cyclic designs’, Discrete Math. 20 (1977), 63–68.Google Scholar
Miao, Y. and Zhu, L., ‘Perfect Mendelsohn designs with block size six’, Discrete Math. 143 (1995), 189–207.Google Scholar
Nilrat, C. and Praeger, C. E., ‘Balanced directed cycle designs based on cyclic groups’, J. Aust. Math. Soc. 58 (1995), 210–218.Google Scholar
Praeger, C. E., ‘Balanced directed cycle designs based on groups’, Discrete Math. 92 (1991), 275–290.Google Scholar
Thomson, A. and Zhou, S., ‘Frobenius circulant graphs of valency four’, J. Aust. Math. Soc. 85 (2008), 269–282.Google Scholar
Thomson, A. and Zhou, S., ‘Frobenius circulant graphs of valency six, Eisenstein–Jacobi networks, and hexagonal meshes’, European J. Combin. 38 (2014), 61–78.Google Scholar
Thomson, A. and Zhou, S., ‘Rotational circulant graphs’, Discrete Appl. Math. 162 (2014), 296–305.Google Scholar
Wilcox, S., ‘Reduction of the Hall–Paige conjecture to sporadic simple groups’, J. Algebra 321(5) (2009), 1407–1428.CrossRefGoogle Scholar
Yin, J., ‘The existence of (v, 6, 3)-PMDs’, Math. Appl. 6 (1993), 457–462.Google Scholar
Zhang, X., ‘Constructions of resolvable Mendelsohn designs’, Ars Combin. 34 (1992), 225–250.Google Scholar
Zhang, X., ‘On the existence of (v, 4, 1)-RPMD’, Ars Combin. 42 (1996), 3–31.Google Scholar
Zhang, X., ‘A few more RPMDs with k = 4’, Ars Combin. 74 (2005), 187–200.Google Scholar
Zhou, S., ‘A class of arc-transitive Cayley graphs as models for interconnection networks’, SIAM J. Discrete Math. 23 (2009), 694–714.Google Scholar