Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T16:56:43.705Z Has data issue: false hasContentIssue false
  • English
  • Français

A REMARK ON THE TRACIAL ROKHLIN PROPERTY

Part of: Selfadjoint operator algebras

Published online by Cambridge University Press:  07 March 2018

YUAN HANG ZHANG
YUAN HANG ZHANG*
Affiliation:
School of Mathematics, Jilin University, Changchun 130012, PR China email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

To explore the difficulties of classifying actions with the tracial Rokhlin property using K-theoretic data, we construct two 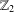$\mathbb{Z}_{2}$ actions 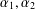$\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2}$ on a simple unital AF algebra 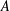$A$ such that 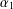$\unicode[STIX]{x1D6FC}_{1}$ has the tracial Rokhlin property and 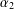$\unicode[STIX]{x1D6FC}_{2}$ does not, while 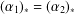$(\unicode[STIX]{x1D6FC}_{1})_{\ast }=(\unicode[STIX]{x1D6FC}_{2})_{\ast }$, where 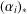$(\unicode[STIX]{x1D6FC}_{i})_{\ast }$ is the induced map by 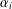$\unicode[STIX]{x1D6FC}_{i}$ acting on 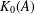$K_{0}(A)$ for 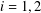$i=1,2$.

Keywords

AF algebraautomorphism of order 2real rank zerotracial Rokhlin property

MSC classification

Primary: 46L05: General theory of $C^*$-algebras
Secondary: 46L35: Classifications of $C^*$-algebras
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 97 , Issue 3 , June 2018 , pp. 492 - 498
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

References

Barlak, S. and Szabó, G., ‘Rokhlin actions of finite groups on UHF-absorbing C ∗ -algebras’, Trans. Amer. Math. Soc. 369(2) (2017), 833–859.CrossRefGoogle Scholar
Blackadar, B., K-Theory for Operator Algebras, Mathematical Sciences Research Institute Publications, 5 (Springer, New York, 1986).Google Scholar
Blackadar, B., ‘Symmetries of the CAR algebra’, Ann. of Math. (2) 131(3) (1990), 589–623.Google Scholar
Blackadar, B. and Rørdam, M., ‘Extending states on preordered semigroups and the existence of quasitraces on C ∗ -algebras’, J. Algebra 152(1) (1992), 240–247.Google Scholar
Bratteli, O., Elliott, G. A., Evans, D. E. and Kishimoto, A., ‘Finite group actions on AF algebras obtained by folding the interval’, K-Theory 8(5) (1994), 443–464.Google Scholar
Connes, A., ‘Outer conjugacy classes of automorphisms of factors’, Ann. Sci. Éc. Norm. Supér. (4) 8(3) (1975), 383–419.Google Scholar
Echterhoff, S., Lück, W., Phillips, N. C. and Walters, S., ‘The structure of crossed products of irrational rotation algebras by finite subgroups of SL2(ℤ)’, J. reine angew. Math. 639 (2010), 173–221.Google Scholar
Elliott, G. A. and Gong, G., ‘On the classification of C ∗ -algebras of real rank zero. II’, Ann. of Math. (2) 144(3) (1996), 497–610.CrossRefGoogle Scholar
Elliott, G. A., Gong, G., Lin, H. and Niu, Z., ‘The classification of simple separable unital 𝓩-stable locally ASH algebras’, J. Funct. Anal. 272(12) (2017), 5307–5359.CrossRefGoogle Scholar
Elliott, G. A. and Su, H., ‘ K-theoretic classification for inductive limit Z 2 actions on AF algebras’, Canad. J. Math. 48(5) (1996), 946–958.Google Scholar
Goodearl, K. R., ‘Notes on a class of simple C ∗ -algebras with real rank zero’, Publ. Mat. 36(2A) (1992), 637–654.CrossRefGoogle Scholar
Handelman, D. and Rossmann, W., ‘Actions of compact groups on AF C ∗ -algebras’, Illinois J. Math. 29(1) (1985), 51–95.CrossRefGoogle Scholar
Herman, R. H. and Jones, V. F. R., ‘Period two automorphisms of UHF C ∗ -algebras’, J. Funct. Anal. 45(2) (1982), 169–176.Google Scholar
Izumi, M., ‘Finite group actions on C ∗ -algebras with the Rohlin property. I’, Duke Math. J. 122(2) (2004), 233–280.Google Scholar
Izumi, M., ‘Finite group actions on C ∗ -algebras with the Rohlin property. II’, Adv. Math. 184(1) (2004), 119–160.CrossRefGoogle Scholar
Kirchberg, E. and Winter, W., ‘Covering dimension and quasidiagonality’, Int. J. Math. 15(1) (2004), 63–85.Google Scholar
Kishimoto, A., ‘Outer automorphisms and reduced crossed products of simple C ∗ -algebras’, Comm. Math. Phys. 81(3) (1981), 429–435.Google Scholar
Lin, H., An Introduction to the Classification of Amenable C∗ -Algebras (World Scientific, River Edge, NJ, 2001).Google Scholar
Lin, H., ‘Classification of simple C ∗ -algebras of tracial topological rank zero’, Duke Math. J. 125(1) (2004), 91–119.Google Scholar
Nawata, N., ‘Finite group actions on certain stably projectionless C ∗ -algebras with the Rohlin property’, Trans. Amer. Math. Soc. 368(1) (2016), 471–493.Google Scholar
Phillips, N. C., ‘An introduction to crossed product $C^{\ast }$ -algebras and minimal dynamics’, http://pages.uoregon.edu/ncp/Courses/CRMCrPrdMinDyn/CRMCrPrdMinDyn.html.Google Scholar
Phillips, N. C., ‘The tracial Rokhlin property for actions of finite groups on C ∗ -algebras’, Amer. J. Math. 133(3) (2011), 581–636.Google Scholar
Phillips, N. C., ‘Finite cyclic group actions with the tracial Rokhlin property’, Trans. Amer. Math. Soc. 367(8) (2015), 5271–5300.CrossRefGoogle Scholar
Rørdam, M., ‘Classification of nuclear, simple C ∗ -algebras’, in: Classification of Nuclear C ∗ -Algebras. Entropy in Operator Algebras, Encyclopaedia of Mathematical Sciences, 126 (Springer, Berlin, 2002), 1–145.Google Scholar
Rosenberg, J., ‘Appendix to O. Bratteli’s paper on “Crossed products of UHF algebras by product type actions”’, Duke Math. J. 46(1) (1979), 25–26; Duke Math. J. 46(1) (1979), 1–23.Google Scholar
Villadsen, J., ‘The range of the Elliott invariant’, J. reine angew. Math. 462 (1995), 31–55.Google Scholar
Williams, D. P., Crossed Products of C ∗ -Algebras, Mathematical Surveys and Monographs, 134 (American Mathematical Society, Providence, RI, 2007).CrossRefGoogle Scholar
Winter, W., ‘Decomposition rank of subhomogeneous C ∗ -algebras’, Proc. Lond. Math. Soc. (3) 89(2) (2004), 427–456.Google Scholar
Winter, W., ‘Decomposition rank and 𝓩-stability’, Invent. Math. 179(2) (2010), 229–301.Google Scholar