Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T20:42:20.478Z Has data issue: false hasContentIssue false
  • English
  • Français

A REMARK ON THE SEPARABLE QUOTIENT PROBLEM FOR TOPOLOGICAL GROUPS

Part of: Normed linear spaces and Banach spaces; Banach lattices Topological and differentiable algebraic systems

Published online by Cambridge University Press:  03 June 2019

SIDNEY A. MORRIS Open the ORCID record for SIDNEY A. MORRIS [Opens in a new window]
SIDNEY A. MORRIS*
Affiliation:
Department of Mathematics and Statistics, La Trobe University, Melbourne, Victoria, 3086, Australia Center for Informatics and Applied Optimization, Federation University Australia, PO Box 663, Ballarat, Victoria, 3353, Australia email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Banach–Mazur separable quotient problem asks whether every infinite-dimensional Banach space 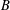$B$ has a quotient space that is an infinite-dimensional separable Banach space. The question has remained open for over 80 years, although an affirmative answer is known in special cases such as when 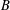$B$ is reflexive or even a dual of a Banach space. Very recently, it has been shown to be true for dual-like spaces. An analogous problem for topological groups is: Does every infinite-dimensional (in the topological sense) connected (Hausdorff) topological group 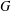$G$ have a quotient topological group that is infinite dimensional and metrisable? While this is known to be true if 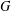$G$ is the underlying topological group of an infinite-dimensional Banach space, it is shown here to be false even if 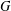$G$ is the underlying topological group of an infinite-dimensional locally convex space. Indeed, it is shown that the free topological vector space on any countably infinite 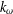$k_{\unicode[STIX]{x1D714}}$-space is an infinite-dimensional toplogical vector space which does not have any quotient topological group that is infinite dimensional and metrisable. By contrast, the Graev free abelian topological group and the Graev free topological group on any infinite connected Tychonoff space, both of which are connected topological groups, are shown here to have the tubby torus 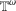$\mathbb{T}^{\unicode[STIX]{x1D714}}$, which is an infinite-dimensional metrisable group, as a quotient group.

Keywords

topological groupquotient groupfree locally convex spacetubby torus groupseparable quotient problem

MSC classification

Primary: 22A05: Structure of general topological groups
Secondary: 46B26: Nonseparable Banach spaces
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 100 , Issue 3 , December 2019 , pp. 453 - 457
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

References

Argyros, S. A., Dodos, P. and Kanellopoulos, V., ‘Unconditional families in Banach spaces’, Math. Ann. 341 (2008), 15–38.Google Scholar
Flood, J., Free Locally Convex Spaces, Dissertationes Math. CCXXI (PWN, Warczawa, 1984).Google Scholar
Franklin, S. P. and Smith Thomas, B. V., ‘A survey of k 𝜔 -spaces’, Topology Proc. 2 (1977), 111–124.Google Scholar
Gabriyelyan, S., ‘The k-space property for free locally convex spaces’, Canad. Math. Bull. 57 (2014), 803–809.Google Scholar
Gabriyelyan, S. S. and Morris, S. A., ‘Free topological vector spaces’, Topology Appl. 223 (2017), 30–49.Google Scholar
Gabriyelyan, S. S. and Morris, S. A., ‘A topological group observation on the Banach–Mazur separable quotient problem’, Topol. Appl. 259 (2019), 283–286.Google Scholar
Hewitt, E. and Ross, K. A., Abstract Harmonic Analysis I (Springer, Berlin, Heidelberg, 1963).Google Scholar
Hofmann, K. H. and Morris, S. A., The Structure of Compact Groups, 3rd edn (De Gruyter, Berlin, Boston, 2013).Google Scholar
Morris, S. A., ‘Varieties of topological groups’, Bull. Aust. Math. Soc. 1 (1969), 145–160.Google Scholar
Morris, S. A., Pontryagin Duality and the Structure of Locally Compact Abelian Groups (Cambridge University Press, London–New York, 1977).Google Scholar
Morris, S. A., ‘Free abelian topological groups’, in: Categorical Topology, Proc. Conf., Toledo, Ohio 1983 (Heldermann, Berlin, 1984), 375–391.Google Scholar
van Mill, J., The Infinite-Dimensional Topology of Function Spaces (Elsevier, North-Holland, Amsterdam, 2006).Google Scholar