Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-19T02:53:12.867Z Has data issue: false hasContentIssue false
  • English
  • Français

REFINEMENTS OF THE FIRST AND SECOND POSITIVE CRANK MOMENTS

Part of: Additive number theory; partitions

Published online by Cambridge University Press:  17 February 2016

JISUN HUH  and
EUNSUNG LIM
JISUN HUH*
Affiliation:
Department of Mathematics, Yonsei University, Seoul 120-749, Republic of Korea email [email protected]
EUNSUNG LIM
Affiliation:
Department of Mathematics, Yonsei University, Seoul 120-749, Republic of Korea email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We revisit Berkovich and Garvan’s two bijections: the first gives symmetry of cranks and the second relates partitions with crank 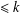$\leq k$ to those with 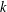$k$ in the rank-set of partitions. Using these, we give a combinatorial proof for the relationship between the first positive crank moment and the sum of sizes of Durfee squares. We also study refinements of the first and second positive crank moments.

Keywords

positive crank momentrank-setrefinement

MSC classification

Primary: 11P82: Analytic theory of partitions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 94 , Issue 2 , October 2016 , pp. 236 - 244
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Andrews, G. E., Chan, S. H. and Kim, B., ‘The odd moments of ranks and cranks’, J. Combin. Theory Ser. A 120 (2013), 77–91.Google Scholar
Andrews, G. E. and Garvan, F. G., ‘Dyson’s crank of a partition’, Bull. Amer. Math. Soc. 18 (1988), 167–171.Google Scholar
Berkovich, A. and Garvan, F. G., ‘Some observations on Dyson’s new symmetries of partitions’, J. Combin. Theory Ser. A 100 (2002), 61–93.Google Scholar
Dyson, F. J., ‘Mappings and symmetries of partitions’, J. Combin. Theory Ser. A 51 (1989), 169–180.Google Scholar
Garvan, F. G., Generalizations of Dyson’s Rank, PhD Thesis, Pennsylvania State University, 1986.Google Scholar