Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T13:20:05.755Z Has data issue: false hasContentIssue false
  • English
  • Français

RAMANUJAN CAYLEY GRAPHS OF FROBENIUS GROUPS

Part of: Graph theory Multiplicative number theory Zeta and $L$-functions: analytic theory

Published online by Cambridge University Press:  26 September 2016

MIKI HIRANO ,
KOHEI KATATA  and
YOSHINORI YAMASAKI
MIKI HIRANO
Affiliation:
Graduate School of Science and Engineering, Ehime University, Bunkyo-cho, Matsuyama, 790-8577, Japan email [email protected]
KOHEI KATATA
Affiliation:
Graduate School of Science and Engineering, Ehime University, Bunkyo-cho, Matsuyama, 790-8577, Japan email [email protected]
YOSHINORI YAMASAKI*
Affiliation:
Graduate School of Science and Engineering, Ehime University, Bunkyo-cho, Matsuyama, 790-8577, Japan email [email protected]
*
✉ [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We determine a bound for the valency in a family of dihedrants of twice odd prime orders which guarantees that the Cayley graphs are Ramanujan graphs. We take two families of Cayley graphs with the underlying dihedral group of order 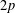$2p$ : one is the family of all Cayley graphs and the other is the family of normal ones. In the normal case, which is easier, we discuss the problem for a wider class of groups, the Frobenius groups. The result for the family of all Cayley graphs is similar to that for circulants: the prime 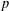$p$ is ‘exceptional’ if and only if it is represented by one of six specific quadratic polynomials.

Keywords

Ramanujan graphFrobenius groupdihedral groupHardy–Littlewood conjecture

MSC classification

Primary: 05C50: Graphs and linear algebra (matrices, eigenvalues, etc.)
Secondary: 05C25: Graphs and abstract algebra (groups, rings, fields, etc.) 11M41: Other Dirichlet series and zeta functions 11N32: Primes represented by polynomials; other multiplicative structure of polynomial values
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 94 , Issue 3 , December 2016 , pp. 373 - 383
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Alon, N. and Roichman, Y., ‘Random Cayley graphs and expanders’, Random Structures Algorithms 5 (1994), 271–284.Google Scholar
Babai, L., ‘Spectra of Cayley Graphs’, J. Combin. Theory Ser. B 27 (1979), 180–189.Google Scholar
Curtis, C. and Reiner, I., Methods of Representation Theory. Vol. I. With Applications to Finite Groups and Orders, Pure and Applied Mathematics (Wiley-Interscience, John Wiley and Sons, New York, 1981).Google Scholar
Hardy, G. H. and Littlewood, J. E., ‘Some problems of ‘partitio numerorum’, III: On the expression of a number as a sum of primes’, Acta Math. 44 (1923), 1–70.Google Scholar
Hirano, M., Katata, K. and Yamasaki, Y., ‘Ramanujan circulant graphs and the conjecture of Hardy–Littlewood and Bateman–Horn’, submitted, 2016.Google Scholar
Lubotzky, A., ‘Expander graphs in pure and applied mathematics’, Bull. Amer. Math. Soc. (N.S.) 49 (2012), 113–162.Google Scholar
Sunada, T., ‘ L-functions in geometry and some applications’, in: Proc. Taniguchi Symp. (1985), Curvature and Topology of Riemannian Manifolds, Lecture Notes in Mathematics, 1201 (Springer, Berlin, 1986), 266–284.Google Scholar
Sunada, T., ‘Fundamental groups and Laplacians’, in: Proc. Taniguchi Symp. (1987), Geometry and Analysis on Manifolds, Lecture Notes in Mathematics, 1339 (Springer, Berlin, 1988), 248–277.Google Scholar
Terras, A., Zeta Functions of Graphs, A Stroll Through the Garden, Cambridge Studies in Advanced Mathematics, 128 (Cambridge University Press, Cambridge, 2011).Google Scholar