Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T06:10:49.293Z Has data issue: false hasContentIssue false
  • English
  • Français

THE QUOTIENT SET OF 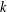$k$-GENERALISED FIBONACCI NUMBERS IS DENSE IN 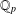$\mathbb{Q}_{p}$

Part of: Sequences and sets

Published online by Cambridge University Press:  09 January 2017

CARLO SANNA
CARLO SANNA*
Affiliation:
Department of Mathematics, Università degli Studi di Torino, Turin, Italy email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The quotient set of 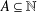$A\subseteq \mathbb{N}$ is defined as 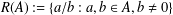$R(A):=\{a/b:a,b\in A,b\neq 0\}$. Using algebraic number theory in 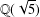$\mathbb{Q}(\sqrt{5})$, Garcia and Luca [‘Quotients of Fibonacci numbers’, Amer. Math. Monthly, to appear] proved that the quotient set of Fibonacci numbers is dense in the 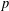$p$-adic numbers 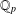$\mathbb{Q}_{p}$ for all prime numbers 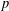$p$. For any integer 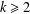$k\geq 2$, let 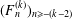$(F_{n}^{(k)})_{n\geq -(k-2)}$ be the sequence of $k$-generalised Fibonacci numbers, defined by the initial values 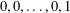$0,0,\ldots ,0,1$ (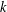$k$ terms) and such that each successive term is the sum of the 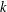$k$ preceding terms. We use 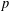$p$-adic analysis to generalise the result of Garcia and Luca, by proving that the quotient set of 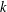$k$-generalised Fibonacci numbers is dense in 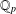$\mathbb{Q}_{p}$ for any integer 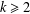$k\geq 2$ and any prime number 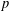$p$.

Keywords

Fibonacci numbersk-generalised Fibonacci numbersp-adic numbersdensity

MSC classification

Primary: 11B39: Fibonacci and Lucas numbers and polynomials and generalizations
Secondary: 11B37: Recurrences 11B05: Density, gaps, topology
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 96 , Issue 1 , August 2017 , pp. 24 - 29
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

References

Brown, B., Dairyko, M., Garcia, S. R., Lutz, B. and Someck, M., ‘Four quotient set gems’, Amer. Math. Monthly 121(7) (2014), 590–599.Google Scholar
Brumer, A., ‘On the units of algebraic number fields’, Mathematika 14 (1967), 121–124.Google Scholar
Bukor, J., Šalát, T. and Tóth, J. T., ‘Remarks on R-density of sets of numbers’, Tatra Mt. Math. Publ. 11 (1997), 159–165.Google Scholar
Dresden, G. P. B. and Du, Z., ‘A simplified Binet formula for k-generalized Fibonacci numbers’, J. Integer Seq. 17(4) (2014), Article 14.4.7, 9 pages.Google Scholar
Everest, G., van der Poorten, A., Shparlinski, I. and Ward, T., Recurrence Sequences, Mathematical Surveys and Monographs, 104 (American Mathematical Society, Providence, RI, 2003).Google Scholar
Fuchs, C., Hutle, C., Luca, F. and Szalay, L., ‘Diophantine triples and $k$ -generalized Fibonacci sequences’, Bull. Malays. Math. Sci. Soc., to appear, doi:10.1007/s40840-016-0405-4.CrossRefGoogle Scholar
Garcia, S. R., Hong, Y. X., Luca, F., Pinsker, E., Schechter, E. and Starr, A., ‘ $p$ -adic quotient sets’ (under review), arXiv:1607.07951.Google Scholar
Garcia, S. R. and Luca, F., ‘Quotients of Fibonacci numbers’, Amer. Math. Monthly, to appear.Google Scholar
Gouvêa, F. Q., p-adic Numbers: An Introduction, 2nd edn, Universitext (Springer, Berlin, 1997).CrossRefGoogle Scholar
Hobby, D. and Silberger, D. M., ‘Quotients of primes’, Amer. Math. Monthly 100(1) (1993), 50–52.Google Scholar
Lengyel, T., ‘The order of the Fibonacci and Lucas numbers’, Fibonacci Quart. 33(3) (1995), 234–239.Google Scholar
Mignotte, M., ‘Sur les conjugués des nombres de Pisot’, C. R. Acad. Sci. Paris Sér. I Math. 298(2) (1984), 21.Google Scholar
Ribenboim, P., My Numbers, My Friends: Popular Lectures on Number Theory (Springer, New York, 2000).Google Scholar
Sanna, C., ‘The p-adic valuation of Lucas sequences’, Fibonacci Quart. 54(2) (2016), 118–124.Google Scholar
Strauch, O. and Tóth, J. T., ‘Asymptotic density of A ⊂N and density of the ratio set R (A)’, Acta Arith. 87(1) (1998), 67–78.Google Scholar
Wolfram, D. A., ‘Solving generalized Fibonacci recurrences’, Fibonacci Quart. 36(2) (1998), 129–145.Google Scholar
Yabuta, M., ‘A simple proof of Carmichael’s theorem on primitive divisors’, Fibonacci Quart. 39(5) (2001), 439–443.Google Scholar