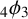1. Introduction
In 2003, Rodriguez-Villegas [Reference Rodriguez-Villegas, Yui and Lewis5] investigated hypergeometric families of Calabi–Yau manifolds. He observed numerically some remarkable supercongruences between the values of the truncated hypergeometric series and expressions derived from the number of
![]() $\mathbb {F}_p$
-points of the associated Calabi–Yau manifolds. For manifolds of dimension
$\mathbb {F}_p$
-points of the associated Calabi–Yau manifolds. For manifolds of dimension
![]() $d=1$
, he conjectured four interesting supercongruences associated to certain elliptic curves, one of which is
$d=1$
, he conjectured four interesting supercongruences associated to certain elliptic curves, one of which is
 $$ \begin{align} \sum_{k=0}^{p-1} \frac{{2k\choose k}^2}{16^k}\equiv (-1)^{({p-1)}/{2}} \pmod{p^2}, \end{align} $$
$$ \begin{align} \sum_{k=0}^{p-1} \frac{{2k\choose k}^2}{16^k}\equiv (-1)^{({p-1)}/{2}} \pmod{p^2}, \end{align} $$
where
![]() $p\ge 5$
is a prime. The conjectural supercongruence (1.1) was first proved by Mortenson [Reference Mortenson4].
$p\ge 5$
is a prime. The conjectural supercongruence (1.1) was first proved by Mortenson [Reference Mortenson4].
For polynomials
![]() $A_1(q), A_2(q),P(q)\in \mathbb {Z}[q]$
, the q-congruence
$A_1(q), A_2(q),P(q)\in \mathbb {Z}[q]$
, the q-congruence
is understood as
![]() $A_1(q)$
is divisible by
$A_1(q)$
is divisible by
![]() $P(q)$
, and
$P(q)$
, and
![]() $A_2(q)$
is coprime with
$A_2(q)$
is coprime with
![]() $P(q)$
. In general, for rational functions
$P(q)$
. In general, for rational functions
![]() $A(q),B(q)\in \mathbb {Q}(q)$
and polynomial
$A(q),B(q)\in \mathbb {Q}(q)$
and polynomial
![]() $P(q)\in \mathbb {Z}[q]$
,
$P(q)\in \mathbb {Z}[q]$
,
Guo and Zeng [Reference Guo and Zeng3, Corollary 2.2] established a q-analogue of (1.1) as follows:
 $$ \begin{align*} \sum_{k=0}^{p-1}\frac{(q;q^2)_k^2}{(q^2;q^2)_k^2}\equiv (-1)^{{(p-1)}/{2}}q^{{(1-p^2)}/{4}} \pmod{[p]^2}. \end{align*} $$
$$ \begin{align*} \sum_{k=0}^{p-1}\frac{(q;q^2)_k^2}{(q^2;q^2)_k^2}\equiv (-1)^{{(p-1)}/{2}}q^{{(1-p^2)}/{4}} \pmod{[p]^2}. \end{align*} $$
Here and in what follows, the q-analogue of the natural number n is defined by
![]() $[n]=(1-q^n)/(1-q)$
, and for
$[n]=(1-q^n)/(1-q)$
, and for
![]() $n\ge 1$
, the q-shifted factorial is defined by
$n\ge 1$
, the q-shifted factorial is defined by
![]() $(a;q)_n=(1-a)(1-aq)\cdots (1-aq^{n-1})$
with
$(a;q)_n=(1-a)(1-aq)\cdots (1-aq^{n-1})$
with
![]() $(a;q)_0=1$
.
$(a;q)_0=1$
.
In 2011, Sun [Reference Sun7, Conjecture 5.5] conjectured a supercongruence related to (1.1): modulo
![]() $p^2$
,
$p^2$
,
 $$ \begin{align} \sum_{k=0}^{(p-1)/2}\frac{{2k\choose k}^2}{32^k}\equiv \begin{cases} \displaystyle 2x-\frac{p}{2x}&\text{if}\ p\equiv 1\pmod{4} \text{ and}\ p=x^2+y^2 \text{ with}\ 4\mid (x-1),\\ 0 &\text{if}\ p\equiv 3\pmod{4}, \end{cases} \end{align} $$
$$ \begin{align} \sum_{k=0}^{(p-1)/2}\frac{{2k\choose k}^2}{32^k}\equiv \begin{cases} \displaystyle 2x-\frac{p}{2x}&\text{if}\ p\equiv 1\pmod{4} \text{ and}\ p=x^2+y^2 \text{ with}\ 4\mid (x-1),\\ 0 &\text{if}\ p\equiv 3\pmod{4}, \end{cases} \end{align} $$
which was proved by Tauraso [Reference Tauraso8] and Sun [Reference Sun6, Theorem 2.2].
Guo and Zeng [Reference Guo and Zeng3, Corollary 2.7] established a partial q-analogue of (1.2):
 $$ \begin{align} \sum_{k=0}^{(p-1)/2}\frac{(q;q^2)_k^2}{(q^2;q^2)_k (q^4;q^4)_k}q^{2k}\equiv 0\pmod{[p]^2} \end{align} $$
$$ \begin{align} \sum_{k=0}^{(p-1)/2}\frac{(q;q^2)_k^2}{(q^2;q^2)_k (q^4;q^4)_k}q^{2k}\equiv 0\pmod{[p]^2} \end{align} $$
for all primes
![]() $p\equiv 3\pmod {4}$
.
$p\equiv 3\pmod {4}$
.
To continue the q-story of (1.2), we recall some q-series notation. The basic hypergeometric series is defined by
 $$ \begin{align*} {}_{r+1}\phi_{r}\bigg[ \begin{matrix} a_1,a_2,\ldots,a_{r+1}\\[5pt] b_1,b_2,\ldots,b_r\end{matrix};q,z\bigg]= \sum_{k=0}^{\infty}\frac{(a_1,a_2,\ldots,a_{r+1};q)_k}{(q,b_1,b_2,\ldots,b_r;q)_k}z^k, \end{align*} $$
$$ \begin{align*} {}_{r+1}\phi_{r}\bigg[ \begin{matrix} a_1,a_2,\ldots,a_{r+1}\\[5pt] b_1,b_2,\ldots,b_r\end{matrix};q,z\bigg]= \sum_{k=0}^{\infty}\frac{(a_1,a_2,\ldots,a_{r+1};q)_k}{(q,b_1,b_2,\ldots,b_r;q)_k}z^k, \end{align*} $$
where
![]() $(a_1,a_2,\ldots ,a_{m};q)_k=(a_1;q)_k(a_2;q)_k\cdots (a_m;q)_k$
. The nth cyclotomic polynomial is given by
$(a_1,a_2,\ldots ,a_{m};q)_k=(a_1;q)_k(a_2;q)_k\cdots (a_m;q)_k$
. The nth cyclotomic polynomial is given by
 $$ \begin{align*} \Phi_n(q)=\prod_{\substack{1\le k \le n\\[3pt](n,k)=1}} (q-\zeta^k), \end{align*} $$
$$ \begin{align*} \Phi_n(q)=\prod_{\substack{1\le k \le n\\[3pt](n,k)=1}} (q-\zeta^k), \end{align*} $$
where
![]() $\zeta $
denotes a primitive nth root of unity.
$\zeta $
denotes a primitive nth root of unity.
The motivation for this paper is to extend the q-congruence (1.3) of Guo and Zeng, and establish a complete q-analogue of (1.2).
Theorem 1.1. Let n be an odd positive integer. Then, modulo
![]() $\Phi _n(q)^2$
,
$\Phi _n(q)^2$
,
 $$ \begin{align} \sum_{k=0}^{(n-1)/2} & \frac{(q;q^2)_k^2}{(q^2;q^2)_k (q^4;q^4)_k}q^{2k}\notag\\[5pt] &\equiv \begin{cases} \displaystyle (-1)^{(n-1)/4}q^{(n-1)(n+3)/8}\frac{(q^2;q^4)_{(n-1)/4}}{(q^4;q^4)_{(n-1)/4}} &\text{if}\ n\equiv 1\pmod{4},\\ 0 &\text{if}\ n\equiv 3\pmod{4}. \end{cases} \end{align} $$
$$ \begin{align} \sum_{k=0}^{(n-1)/2} & \frac{(q;q^2)_k^2}{(q^2;q^2)_k (q^4;q^4)_k}q^{2k}\notag\\[5pt] &\equiv \begin{cases} \displaystyle (-1)^{(n-1)/4}q^{(n-1)(n+3)/8}\frac{(q^2;q^4)_{(n-1)/4}}{(q^4;q^4)_{(n-1)/4}} &\text{if}\ n\equiv 1\pmod{4},\\ 0 &\text{if}\ n\equiv 3\pmod{4}. \end{cases} \end{align} $$
The important ingredients in the proof of (1.4) include Andrews’
![]() $_4\phi _3$
terminating identity [Reference Gasper and Rahman2, (II.17), page 355]:
$_4\phi _3$
terminating identity [Reference Gasper and Rahman2, (II.17), page 355]:
 $$ \begin{align} {}_{4}\phi_{3}\bigg[ \begin{matrix} q^{-n},a^2q^{n+1},c,-c\\[5pt] aq,-aq,c^2\end{matrix};q,q\bigg] =\begin{cases} 0 &\text{if}\ n\equiv 1\pmod{2},\\ \displaystyle \frac{c^n(q,a^2q^2/c^2;q^2)_{n/2}}{(a^2q^2,c^2q;q^2)_{n/2}} &\text{if}\ n\equiv 0\pmod{2}. \end{cases} \end{align} $$
$$ \begin{align} {}_{4}\phi_{3}\bigg[ \begin{matrix} q^{-n},a^2q^{n+1},c,-c\\[5pt] aq,-aq,c^2\end{matrix};q,q\bigg] =\begin{cases} 0 &\text{if}\ n\equiv 1\pmod{2},\\ \displaystyle \frac{c^n(q,a^2q^2/c^2;q^2)_{n/2}}{(a^2q^2,c^2q;q^2)_{n/2}} &\text{if}\ n\equiv 0\pmod{2}. \end{cases} \end{align} $$
The rest of the paper is organised as follows. In the next section, we shall explain why (1.4) is a q-analogue of (1.2). The proof of Theorem 1.1 will be presented in Section 3.
2. Why (1.4) is a q-analogue of (1.2)
Let p be an odd prime. It is clear that
Setting
![]() $n\to p$
and
$n\to p$
and
![]() $q\to 1$
on both sides of (1.4) gives, modulo
$q\to 1$
on both sides of (1.4) gives, modulo
![]() $p^2$
,
$p^2$
,
 $$ \begin{align} \sum_{k=0}^{(p-1)/2}\frac{{2k\choose k}^2}{32^k} \equiv \begin{cases} \displaystyle \frac{(-1)^{(p-1)/4}}{2^{(p-1)/2}}{(p-1)/2\choose (p-1)/4} &\text{if}\ p\equiv 1\pmod{4},\\ 0 &\text{if}\ p\equiv 3\pmod{4}. \end{cases} \end{align} $$
$$ \begin{align} \sum_{k=0}^{(p-1)/2}\frac{{2k\choose k}^2}{32^k} \equiv \begin{cases} \displaystyle \frac{(-1)^{(p-1)/4}}{2^{(p-1)/2}}{(p-1)/2\choose (p-1)/4} &\text{if}\ p\equiv 1\pmod{4},\\ 0 &\text{if}\ p\equiv 3\pmod{4}. \end{cases} \end{align} $$
By a result due to Chowla et al. [Reference Chowla, Dwork and Evans1],
 $$ \begin{align*} {(p-1)/2\choose (p-1)/4}\equiv \frac{2^{p-1}+1}{2}\bigg(2x-\frac{p}{2x}\bigg)\pmod{p^2}, \end{align*} $$
$$ \begin{align*} {(p-1)/2\choose (p-1)/4}\equiv \frac{2^{p-1}+1}{2}\bigg(2x-\frac{p}{2x}\bigg)\pmod{p^2}, \end{align*} $$
where
![]() $p\equiv 1\pmod {4}$
and
$p\equiv 1\pmod {4}$
and
![]() $p=x^2+y^2$
with
$p=x^2+y^2$
with
![]() $4\mid (x-1)$
. It follows that
$4\mid (x-1)$
. It follows that
 $$ \begin{align} \frac{(-1)^{(p-1)/4}}{2^{(p-1)/2}}{(p-1)/2\choose (p-1)/4} &\equiv (-1)^{(p-1)/4}\frac{2^{p-1}+1}{ 2^{(p+1)/2}}\bigg(2x-\frac{p}{2x}\bigg)\notag\\[5pt] &\equiv 2x-\frac{p}{2x}\pmod{p^2}, \end{align} $$
$$ \begin{align} \frac{(-1)^{(p-1)/4}}{2^{(p-1)/2}}{(p-1)/2\choose (p-1)/4} &\equiv (-1)^{(p-1)/4}\frac{2^{p-1}+1}{ 2^{(p+1)/2}}\bigg(2x-\frac{p}{2x}\bigg)\notag\\[5pt] &\equiv 2x-\frac{p}{2x}\pmod{p^2}, \end{align} $$
where we have used the fact [Reference Sun6, page 1918]:
Combining (2.1) and (2.2), we arrive at (1.2). Thus, (1.4) is indeed a q-analogue of (1.2).
3. Proof of Theorem 1.1
Let n be an odd positive integer. Setting
![]() $n\to (n-1)/2,q\to q^2,a\to 1$
on both sides of (1.5) gives
$n\to (n-1)/2,q\to q^2,a\to 1$
on both sides of (1.5) gives
 $$ \begin{align} \sum_{k=0}^{(n-1)/2}\frac{(q^{1-n},q^{1+n},c,-c;q^2)_k}{(q^2,q^2,-q^2,c^2;q^2)_k}q^{2k} =\begin{cases} \displaystyle \frac{c^{(n-1)/2}(q^2,q^4/c^2;q^4)_{(n-1)/4}}{(q^4,c^2q^2;q^4)_{(n-1)/4}} &\text{if}\ n\equiv 1\pmod{4},\\ 0 &\text{if}\ n\equiv 3\pmod{4}. \end{cases} \end{align} $$
$$ \begin{align} \sum_{k=0}^{(n-1)/2}\frac{(q^{1-n},q^{1+n},c,-c;q^2)_k}{(q^2,q^2,-q^2,c^2;q^2)_k}q^{2k} =\begin{cases} \displaystyle \frac{c^{(n-1)/2}(q^2,q^4/c^2;q^4)_{(n-1)/4}}{(q^4,c^2q^2;q^4)_{(n-1)/4}} &\text{if}\ n\equiv 1\pmod{4},\\ 0 &\text{if}\ n\equiv 3\pmod{4}. \end{cases} \end{align} $$
Letting
![]() $c\to 0$
on both sides of (3.1) and noting that for
$c\to 0$
on both sides of (3.1) and noting that for
![]() $n\equiv 1\pmod {4}$
,
$n\equiv 1\pmod {4}$
,
and
we obtain
 $$ \begin{align} \sum_{k=0}^{(n-1)/2} &\frac{(q^{1-n},q^{1+n};q^2)_k}{(q^2;q^2)_k(q^4;q^4)_k}q^{2k} \notag\\ & =\begin{cases} \displaystyle (-1)^{(n-1)/4}q^{(n-1)(n+3)/8}\frac{(q^2;q^4)_{(n-1)/4}}{(q^4;q^4)_{(n-1)/4}} &\text{if}\ n\equiv 1\pmod{4},\\ 0 &\text{if}\ n\equiv 3\pmod{4}. \end{cases} \end{align} $$
$$ \begin{align} \sum_{k=0}^{(n-1)/2} &\frac{(q^{1-n},q^{1+n};q^2)_k}{(q^2;q^2)_k(q^4;q^4)_k}q^{2k} \notag\\ & =\begin{cases} \displaystyle (-1)^{(n-1)/4}q^{(n-1)(n+3)/8}\frac{(q^2;q^4)_{(n-1)/4}}{(q^4;q^4)_{(n-1)/4}} &\text{if}\ n\equiv 1\pmod{4},\\ 0 &\text{if}\ n\equiv 3\pmod{4}. \end{cases} \end{align} $$
Since
and
![]() $1-q^n\equiv 0\pmod {\Phi _n(q)}$
,
$1-q^n\equiv 0\pmod {\Phi _n(q)}$
,
It follows that
Thus,
 $$ \begin{align} (q^{1-n},q^{1+n};q^2)_k &=\prod_{j=1}^k (1-q^{-n+2j-1})(1-q^{n+2j-1})\notag\\ &\equiv \prod_{j=1}^k (1-q^{2j-1})^2 =(q;q^2)_k^2 \pmod{\Phi_n(q)^2}. \end{align} $$
$$ \begin{align} (q^{1-n},q^{1+n};q^2)_k &=\prod_{j=1}^k (1-q^{-n+2j-1})(1-q^{n+2j-1})\notag\\ &\equiv \prod_{j=1}^k (1-q^{2j-1})^2 =(q;q^2)_k^2 \pmod{\Phi_n(q)^2}. \end{align} $$
Finally, substituting (3.3) into the left-hand side of (3.2) gives, modulo
![]() $\Phi _n(q)^2$
,
$\Phi _n(q)^2$
,
 $$ \begin{align*} \sum_{k=0}^{(n-1)/2} & \frac{(q;q^2)_k^2}{(q^2;q^2)_k(q^4;q^4)_k}q^{2k} \\ & \equiv \begin{cases} \displaystyle (-1)^{(n-1)/4}q^{(n-1)(n+3)/8}\frac{(q^2;q^4)_{(n-1)/4}}{(q^4;q^4)_{(n-1)/4}} &\text{if}\ n\equiv 1\pmod{4},\\ 0 &\text{if}\ n\equiv 3\pmod{4}, \end{cases} \end{align*} $$
$$ \begin{align*} \sum_{k=0}^{(n-1)/2} & \frac{(q;q^2)_k^2}{(q^2;q^2)_k(q^4;q^4)_k}q^{2k} \\ & \equiv \begin{cases} \displaystyle (-1)^{(n-1)/4}q^{(n-1)(n+3)/8}\frac{(q^2;q^4)_{(n-1)/4}}{(q^4;q^4)_{(n-1)/4}} &\text{if}\ n\equiv 1\pmod{4},\\ 0 &\text{if}\ n\equiv 3\pmod{4}, \end{cases} \end{align*} $$
as desired.