Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-30T15:21:36.838Z Has data issue: false hasContentIssue false
  • English
  • Français

The product of vector-valued measures

Published online by Cambridge University Press:  17 April 2009

Charles Swartz
Charles Swartz
Affiliation:
Department of Mathematical Sciences, New Mexico State University, Las Cruces, New Mexico, USA.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let M (N) be a σ–algebra of subsets of a set S (T) and let X, Y be Banach spaces with (,) a continuous bilinear map from X × Y into the scalar field. If μ: M → X (v: N → Y) is a vector measure and λ is the scalar measure defined on the measurable rectangles A × B, A ∈ M, B ∈ N, by λ(A×B) = 〈μ(A), v(B)〉, it is known that λ is generally not countably additive on the algebra generated by the measurable rectangles and therefore has no countably additive extension to the σ-algebra generated by the measurable rectangles. If μ (v) is an indefinite Pettis integral 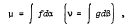it is shown that a necessary and sufficient condition that λ have a countable additive extension to the σ-algebra generated by the measurable rectangles is that the function F: (s, t) → 〈f(s), g(t)〉 is integrable with respect to α × β.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 8 , Issue 3 , June 1973 , pp. 359 - 366
Copyright
Copyright © Australian Mathematical Society 1973

References

[1]Alò, Richard A. and de Korvin, Andre, “A one-sided Fubini theorem for Gowurin measures”, J. Math. Anal. Appl. 38 (1972), 387–398.CrossRefGoogle Scholar
[2]Bartle, R.G., “A general bilinear vector integral”, Studia Math. 15 (1956), 337–352.CrossRefGoogle Scholar
[3]Brooks, J.K., “On the Gelfand-Pettis integral and unconditionally convergent series”, Bull. Acad. Polon. Sci., Sér. Sci. math. astronom. phys. 17 (1969), 809–813.Google Scholar
[4]Dinculeanu, N., Vector measures (Pergamon Press, Oxford, London, Edinburgh, New York, Toronto, Sydney, Paris, Braunschweig, 1967).CrossRefGoogle Scholar
[5]Dudley, R.M. and Pakula, Lewis, “A counter-example on the inner product of measures”, Indiana Univ. Math. J. 21 (1972), 843–845.Google Scholar
[6]Dunford, Nelson and Schwartz, Jacob T., Linear operators, Part I (Interscience [John Wiley & Sons], New York, London, 1958).Google Scholar
[7]Hewitt, Edwin and Stromberg, Karl, Real and abstract analysis (Springer-Verlag, Berlin, Göttingen, Heidelberg, New York, 1965).Google Scholar
[8]Hille, Einar and Phillips, Ralph S., Functional analysis and semigroups (Colloquium Publ. 31, revised ed. Amer. Math. Soc., Providence, Rhode Island, 1957).Google Scholar
[9]Moedomo, S. and Uhl, J.J. Jr, “Radon-Nikodým theorems for the Bochner and Pettis integrals”, Pacific J. Math. 38 (1971), 531–536.Google Scholar
[10]Rao, M. Bhaskara, “Countable additivity of a set function induced by two vector-valued measures”, Indiana Univ. Math. J. 21 (1972), 847–848.CrossRefGoogle Scholar